Теорема 1.2

Достаточные условия локального extr для функции 2^х переменных.

Пусть в стационарной точке X*=(x₁,x₂) и некоторой её окрестности функция Z=f(x₁,x₂) имеет непрерывные частные производные до 2^ого порядка включительно.

Обозначим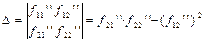

Тогда:

1. Если 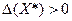, то функция имеет локальныйextr в т.X* (max, если 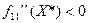, и min, если ).

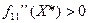2. Если 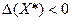, то функция extr в т.X* не имеет.

3. Если 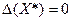, то необходимо дополнительное исследование.

Опр. Функция Z=f(x)=f(x₁,x₂,…x_n) имеет в точке X* заданной области D глобальный max (наибольшее значение), если неравенство f(x)≤f(x*), выполняется для любой точки x€D.

Теорема 1.3 (Вайерштрасса)

Пусть функция Z=f(X) определена и дифференцируема в замкнутой и ограниченной области D, тогда Z достигает в этой области своих наибольших и наименьших значений или в стационарной точке, или в граничной точке области.

Таким образом, чтобы найти наибольшее (наименьшее) значение функции Z=f(X) в обл. D, нужно:

1. Найти все стационарные точки в обл. D и вычислить значение функции.

2. Исследовать функцию на extr на границе обл. D (задача на условный экстремум)

3. Сравнить значение функции, полученной в п.1 и п.2 наибольшее (наименьшее) из этих чисел и будет глобальный max (min) функции в данной области.

Дата добавления: 2015-08-20