Вырожденность в транспортных задачах

При решении транспортной задачи может оказаться, что число занятых клеток меньше, чем M + п - 1. В этом слу­чае задача имеет вырожденное решение. Для возможного его исключения целесообразно поменять местами поставщиков и потребителей или ввести в свободную клетку с наименьшим тарифом нулевую поставку. Нуль помещают в такую клетку, чтобы в каждой строке и каждом столбце было не менее одной занятой клетки.

Рассмотрим вырожденность в транспортной задаче на при­мере.

Пример 2. Фирма осуществляет поставку бутылок на три за­вода, занимающиеся производством прохладительных напит­ков. Она имеет три склада, причем на складе 1 находится 6000 бутылок, на складе 2 — 3 000 бутылок и на складе 3 — 4 000 бутылок. Первому заводу требуется 4000 бутылок, второму за­воду — 5 000 бутылок, третьему заводу — 1000 бутылок. Мат­рицей

Задана стоимость перевозки одной бутылки от каждого склада к каждому заводу.

Как следует организовать доставку бутылок на заводы, чтобы стоимость перевозки была минимальной?

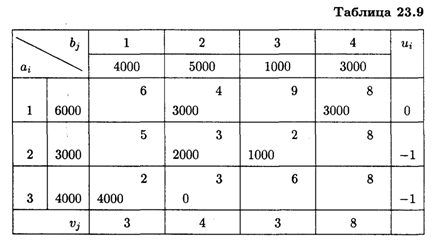
Решение. Запишем исходные данные в распределитель­ную таблицу (табл. 23.9), найдем исходное опорное решение по методу минимального тарифа. Число заполненных клеток равно 5, Т + П - 1 = 6, следовательно, задача является вырож­денной.

Для исключения вырожденности необходимо в какую-то клетку ввести нулевую поставку. Такая клетка становится условно занятой, ее целесообразно определить при вычислении потенциалов занятых клеток, она должна иметь наименьший тариф по сравнению с другими клетками, которые могут быть условно занятыми.

Так, для нахождения потенциала И 3 поместим нулевую по­ставку в клетку (3,2), после чего представляется возможным вычислить остальные потенциалы.

Оценки свободных клеток следующие:

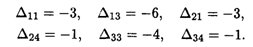
Все оценки отрицательные, получили оптимальное реше­ние:

Таким образом, со склада 1 целесообразно поставить 3000 бутылок второму и четвертому заводам, со склада 2 — 2000 бутылок второму заводу и 1000 бутылок третьему, со склада 3 — 4000 бутылок первому заводу, при этом стои­мость транспортных расходов будет минимальной и составит 28 000 усл. ед.

Дата добавления: 2015-08-20