
Читайте также:
|
Задача НП:
Найти max(min) функции Z=f(x1,x2)→max(min) при ограничениях gi (x1,x2)=0, где f (x1,x2,xn), gi (x1,x2,xn) – непрерывны вмести со своими производными первого порядка.
Эта задача является задачей на условный экстремум.
Определение: Пусть точка Xo =(x1o,x2o … xno) – это точка, удовлетворяющая условию связи (4). Говорят, что в точке Xo функция Z =f(x) имеет условныйmax(min), если существует такая окрестность этой точки, что для всех точек xиз этой окрестности, координаты которых удовлетворяют условию (4), выполняется неравенство:
f (Xo) 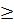 f(x)
f(x)
(f (Xo) 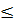 f(x))
f(x))
Z =f(x1,x2)→max(min)
g (x1,x2)=0
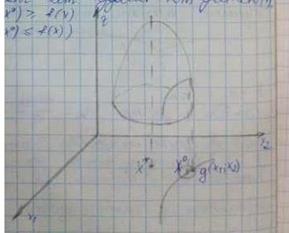
Допустим, что уравнение связи g (x1,x2)=0 удалось разрешить относительно одной из переменных. Например, выразим x2 через x1x2= φ (x1)
Подставив полученное выражение в функцию Z, получим Z =f(x1,φ1(x1)) – функция одной переменной, то есть задача свелась к задаче отыскания extr функции одной переменной.
Пример:
Найти точку экстремума функции Z =x12+2x22→max(min) при условии 3x1+2x2=11
Решение:
Выразим x2 из уравнения 3x1+2x2=11.
x2=(11-3x1)/2.
Тогда Z =x2+2*((11-3x1)/2)2 =11/2*(x12-6x1+11)
Нужно найти точки extrфункции Z = 11/2*(2x-6)=0 при x1=3
x1=3 – точка min, соответственно x2=(11-3x1)/2=(11-3*3)/2=1
Точка (3;1) – условныйmin, Z =32+2*12=11
Замечание1: Аналогично задание (3),(4) сводятся к нахождению extrфункции от отn-m переменных, если удастся из других уравнений связи (4) выразить m переменных через оставшиеся n переменных.
Замечание2: В рассмотренном примере уравнение связи оказалось линейным, поэтому его легко удалось решить относительно одной из переменных.
Дата добавления: 2015-08-20; просмотров: 80 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Нелинейная целевая функция и линейная система ограничений. | | | Метод множителей Лагранжа |