Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Графический метод решения задач нелинейного программирования

Геометрический смысл стандартной ЗЛП. Множество допустимых решений. Графический способ решения. | Приведение открытой ТЗ к закрытой. | Билет.метод потенциалов. | Вырожденность в транспортных задачах | Альтернативный оптимум в транспортных задачах | Целочисленное программирование. Метод Гомори (правильное отсечение, правила формирования правильного отсечения). | Пример. | Графический метод решения задачи целочисленного программирования. | Теорема 1.1 | Условный экстремум. Метод множителей Лагранжа |


Читайте также:
  1. A.1.3. Графический интерфейс
  2. A.1.3.1. Простой графический интерфейс.
  3. B)& В течение 15 дней со дня вручения копии решения, вынесенного судом
  4. B)& До вынесения судом решения по делу
  5. C)& постановление и оглашение решения
  6. Case-метод Баркера
  7. G) Решение о восстановлении утраченного судебного решения.

Задачу НЛП с двумя переменными можно решить графическим методом.

1.Линейная целевая функция и не линейная ограниченная. Z=C1x1+C2x2→max(min)

gi(x1,x2)

Необходимое условие локальногоextr:

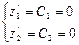
Локального extr линейная функция не имеет, т.е. наиб. (наим.) значения функция может принимать только на границе ОДР.

Пример:

Z=2x1+x2

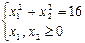
Решение:

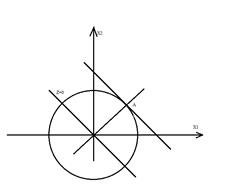
Построим область допустимых решений

2x1+x2=C ;C=0; 2x1+x2=0

Глобальный min равный нулю О(0;0)

Глобальный max в точке А-точка касания линии уровня и окружности.

I способ (для окружности): Проведем через точку А прямую, перпендикулярную касательной. Эта прямая будет проходить через точку О (касательная к окружности перпендикулярна радиусу).

2x1+x2=C → x2=C-2x1, ее угловой коэффициент k=2.

Значит угловой коэффициент прямой ОА (k1*k2=-1) равен ½, т.е. ее уравнение имеет вид: x2=1/2x1+b

Точка О (0;0) принадлежит прямой ОА → b≠0 (ОА): x2=1/2x1

Чтобы найти координаты точка А, нужно решить систему:

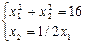
(х должно быть >0)

II способ. Чтобы найти общие точки, нужно решить систему:

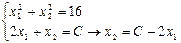
Пример: Z=2x1+x2→max(min)

Одна общая точка ó Квадратное уравнение имеет 1 кореньó Д=(4С)2-20(С2-16)=0

4С2-5(С2-16)=0

С2=80

С=

Дата добавления: 2015-08-20; просмотров: 782 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Теорема 1.2| Нелинейная целевая функция и линейная система ограничений.
mybiblioteka.su - 2015-2024 год. (0.005 сек.)