Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Графический метод решения задачи целочисленного программирования.

Геометрический смысл стандартной ЗЛП. Множество допустимых решений. Графический способ решения. | Приведение открытой ТЗ к закрытой. | Билет.метод потенциалов. | Вырожденность в транспортных задачах | Альтернативный оптимум в транспортных задачах | Целочисленное программирование. Метод Гомори (правильное отсечение, правила формирования правильного отсечения). | Теорема 1.2 | Графический метод решения задач нелинейного программирования | Нелинейная целевая функция и линейная система ограничений. | Условный экстремум. Метод множителей Лагранжа |


Читайте также:
  1. A.1.3. Графический интерфейс
  2. A.1.3.1. Простой графический интерфейс.
  3. B)& В течение 15 дней со дня вручения копии решения, вынесенного судом
  4. B)& До вынесения судом решения по делу
  5. C)& постановление и оглашение решения
  6. Case-метод Баркера
  7. G) Решение о восстановлении утраченного судебного решения.

Число переменных равно 2.

Ограничения в виде неравенств.

Пример:

 

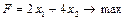
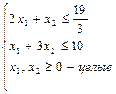
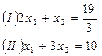
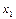
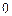
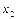
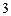
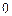
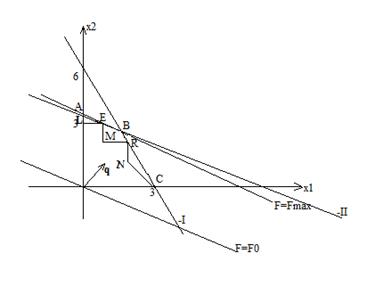
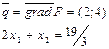
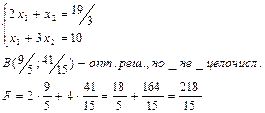строим целочисленную решётку.

Целочисленный оптимум в точке Е (1;3), F=2+12=14-Fmax

 

12. Нелинейное программирование. Постановка задачи. Локальные, глобальные, условные экстремумы. Необходимые условия локального экстремума.

Найти решение X=(x1, x2,…xn) системы ограничений:

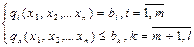, при котором функция цели

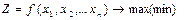принимает наибольшее (наименьшее) значение.

В зависимости от вида целевой функции и системы ограничений разработаны специальные методы для решения задач нелинейного программирования:

1. Метод множителей Лагранджа

2. Квадратичное и выпуклое программирование

3. Градиентные методы

4. Графические методы

5. Различные приближённые методы

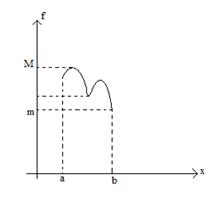
m- наименьшее значение (глобальный min на [a;b])

M- наибольшее значение (глобальный maxна [a;b])

Пусть функция Z=f(x1,x2,…xn)=f(x) определена в точке X*=(x1*,x2*…xn*) и в некоторой её окрестности.

Если для всех точек X из этой окрестности 1. f(X)<f(X*); 2. f(X)>f(X*), то говорят, что функция f имеет локальный экстремум (1. Локальный max; 2. Локальный min)

Дата добавления: 2015-08-20; просмотров: 190 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Пример.| Теорема 1.1
mybiblioteka.su - 2015-2024 год. (0.006 сек.)