Целочисленное программирование. Метод Гомори (правильное отсечение, правила формирования правильного отсечения).

Некоторые задачи линейного программирования требуют целочисленного решения. К ним относятся задачи по произ­водству и распределению неделимой продукции (выпуск стан­ков, телевизоров, автомобилей и т. д.). В общем виде математи­ческая модель задачи целочисленного программирования име­ет вид

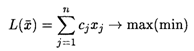
При ограничениях:

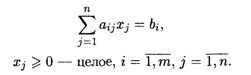
Оптимальное решение задачи, найденное симплексным ме­тодом, часто не является целочисленным. Его можно округлить до ближайших целых чисел. Однако такое округление может дать решение, не лучшее среди целочисленных решений, или привести к решению, не удовлетворяющему системе ограниче­ний. Поэтому для нахождения целочисленного решения нужен особый алгоритм. Такой алгоритм предложен Гомори и состо­ит в следующем.

Симплексным методом находят оптимальное решение за­дачи. Если решение целочисленное, то задача решена. Если же оно содержит хотя бы одну дробную координату, то на­кладывают дополнительное ограничение по целочисленности и вычисления продолжают до получения нового решения. Ес­ли и оно является нецелочисленным, то вновь накладывают дополнительное ограничение по целочисленности. Вычисления продолжают до тех пор, пока не будет получено целочисленное решение или показано, что задача не имеет целочисленного ре­шения.

Пусть получено оптимальное решение 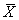Опт = (F 1, F 2,..., Fr, 0,..., 0), которое не является целочисленным, тогда по­следний шаг симплексной таблицы имеет следующий вид:

Где R — ранг системы ограничений; Hi,R+ 1 — коэффициент сим­плексной таблицы I -й строки, (R + 1)-го столбца; Fi — свобод­ный член I -й строки.

Пусть Fi и хотя бы одно Hij (J = 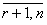, r = 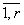) — дроб­ные числа.

Обозначим через [ Fi ] и [ Hij ] целые части чисел Fi и Hij.

Определение 1. Целой частью числа Fi называют наибольшее целое число, не превосходящее числа Fi.

Дробную часть чисел Fi и Hij обозначим { Fi } и { Hij }, она определяется следующим образом:

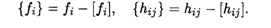
Дата добавления: 2015-08-20