Нелинейная целевая функция и линейная система ограничений.

Z=(x₁-2)²+(x₂-3)²→max(min)

Линия уровня: ((x₁-2)+(x₂-3))²=C

Если С<0 уравнение ничего не определяет, т.е. С>=0, при С=0.

(x₁-2)²+(x₂-3)²=0 – точк (2;3) при С>0

(x₁-2)²+(x₂-3)²=C– уравнение окружности с центром в точке (2;3) и радиусом R=√C

Исследуем функцию на локальныйextr:

А)найдем стационарные точки:

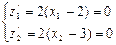x₁=2, x₂=3 (2;3)-стационарные точки

Б)проверим выполнение достаточных условий.

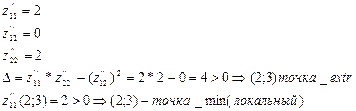
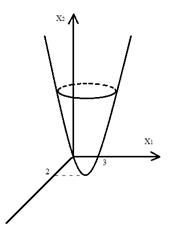
Найдем глобальныйmaxи min. Построим ОДР:

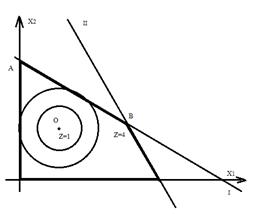I)x₁+2x₂=12; II)x₁+x₂=9

Глобальный min равен 0, достигается в точке О (2;3). Глобальный max функции достигается в точке С (наиболее удаленная точка от О₁) С(9;0) Z(C)=(9-2)²+(0-3)²=58

Пример: Найти глобальныйextrфункции Z=(x₁-6)²+(x₂-3)², при ограничениях

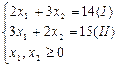
(6;3)-точки глобальногоmin. Построим ОДР:

Глобальный maxв точке О(0;0) Z_max(О)=(0-6)²+(0-3)²=45

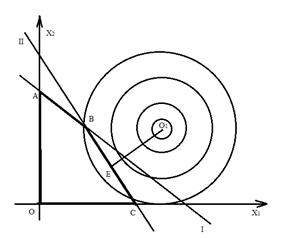
Глобальный min в точке E(прямая IIк прямой OE) – проходящей через точку О перпендикулярная прямой IIx-x₀/m=y-y₀/n

A(x-x₀)+B(y-y₀)=0

(II)=3x₁+2x₂=15

N_II=(3;2)

Уравнение прямойOEx₁-b/3=x₂-3/2

Уравнение (О,Е): 2(x₁-6)+3(x₂-3)

2x₁-3x₂=3; E=(II)∩O,E;

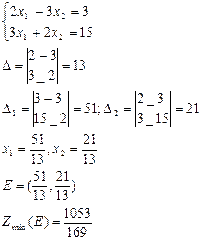
3.Нелинейная целевая функция и нелинейная система ограничений.

Пример: Найти глобальные экстремумы функции Z=(x₁-2)²+(x₂-1)²→max(min)

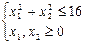
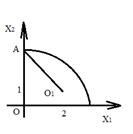
Покажем minО(2;1), Z(О₁)=0

Глобальный minZ=0 в точке О₁(2;1)

Глобальный maxв точке А(0;4)

Z_max(A)=(0-2)²+(4-1)²=13

Пример: Z=x₁²+x₂²→max(min)

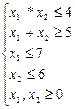
Решение:

ОДР: 1)x₁*x₂=4 – гипербола

2)х₁+х₂=5

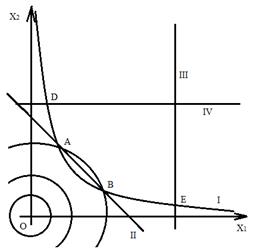Точка О (0;0) не удовлетворяет неравенству х₁+х₂≥5 линии уровня x₁²+x₂²=С, при С=0 – точка О(0;0) при С>0.

x₁²+x₂²=С – окружности с центром в точке О(0;0) и радиусом R=√C

Глобальный minдостигается в точке А и В – точках пересечения (I) и (II)

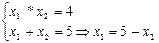
(5-x₂)x₂=4

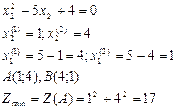
Глобальный max достигается в точке Dи Е – наиболее удаленных точках ОДР от точки О.

Дата добавления: 2015-08-20