
Читайте также:
|
Различные формы задачи ЛП. Переход от стандартной задачи к канонической (допустимое решение (план), оптимальное решение).
Система m линейных уравнений и неравенств с n переменными
а11 X1 + a12X2 + … + а1nXn≤b1
а21 X1 + a22X2 + … + а2nXn≤b2
(1) ………………………………………………….
ак1 X1 + aк2X2 + … + акnXn≤bк
ак1+1,1 X1 + aк+1,2X2 + … + ак+1,nXn≤bк+1
am1 X1 + аm2X2 +…+ аmnxn ≤bm
F=C1x1+C2x2+……+Cnxn (2)
Необходимо найти такое решение Х=(х1,х2,х l …хn), где х i ≥0, i =1͞, l; l ≤n(3), при котором линейная функция (2) принимает оптимальное (max/min) значение.
F= 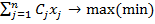
Система:
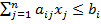 , i =1͞,k
, i =1͞,k
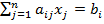 , i =k͞+1, m
, i =k͞+1, m
x j≥ 0, j=1͞, l; l ≤n
Система (1) – система ограничений, F – целевая функция (функция цели)
Опр. Оптимальное решение (оптимальный план) ЗЛП – это решение Х=(х1,х2,х3…хn) системы ограничений (1), удовлетворяющее условию (3), при котором линейная функция (2) принимает оптимальное значение.
Опр. Если все x j ≥0 (j=1͞,n) и система ограничений (1) состоит только из неравенств, то задача называется стандартной.
Опр. Если все x j ≥0 (j=1͞,n) и система ограничений (1) состоит только из уравнений, то задача называется канонической.
Теорема: Все перечисленные формы задач эквивалентны.
Доказательство:
1) стандартная задача→каноническая задача
Рассмотрим новые переменные z1, z2….zm;m=числу ограничений
Рассмотрим каноническую задачу
а11 X1 + a12X2 + … + а1nXn+ z1=b1
а21 X1 + a22X2 + … + а2nXn+z2=b2
……………………………………..
am1 X1 + аm2X2 +…+ аmnxn +zm= bm
x j≥ 0, j=1͞,n; z i ≥0; i =1͞,m
F=C1x1+C2x2+…+Cnxn + 0*z1+0*z2+…+0*zm→max
Пусть Х*=(х1*,х2*,х3*…хn*,z1*,z2*,…zm*) –решение канонической задачи (КЗ),
тогда (х1*,х2*,х3*…хn*) – решение стандартной задачи (СЗ).
Х*– удовлетворяет всем ограничениям СЗ, x j* ≥0 и т.к. z j *≥0, то равенству
а i 1 X1* + a i 2X2* + … + а i n*+ z i *=b i соответствует неравенство а i 1 X1* + a i 2X2* + … + а i n*≤b i
Допустим, что Х* - не является оптимальным решением СЗ, т.е. найдется набор 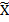 =(
=(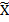 1,
1, 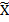 2,…
2,… 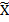 n), который дает большее значение целевой функции, т.е.
n), который дает большее значение целевой функции, т.е.
С1 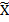 1+С2
1+С2 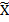 2+…+Сn
2+…+Сn 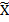 n=C1x1*+C2x2*+…+Cnxn*
n=C1x1*+C2x2*+…+Cnxn*
Покажем, что это невозможно:
Рассмотрим набор (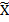 1,
1, 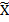 2,…
2,… 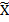 n,
n, 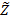 1,
1, 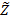 2…
2… 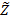 m), где z i = b i – a i 1
m), где z i = b i – a i 1 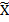 1 – a i 2
1 – a i 2 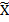 2 – a i n
2 – a i n 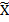 n, т.е. набор удовлетворяет условиям КЗ, но это противоречит оптимальности набора Х*.
n, т.е. набор удовлетворяет условиям КЗ, но это противоречит оптимальности набора Х*.
2) Каноническая→стандартная
а i 1 X1 + a i 2X2 + … + а i n=b i
Система:
а i 1 X1 + a i 2X2 + … + а i n≤ b i
─а i 1 X1 ─ a i 2X2 ─… ─ а i n≤ ─b i
и т.д.
Замечание: в случае, когда в задаче требуется минимизировать линейную функцию, задачу можно свести к задаче максимизации.
Опр. Набор (вектор) Х=(х1,х2,х3…хn), удовлетворяющий всем ограничениям ЗЛП называется допустимым набором (вектором).
Опр. Если множество допустимых решений не пусто, то задача называется допустимой.
Геометрический смысл стандартной ЗЛП. Множество допустимых решений. Графический способ решения.
n=2
Рассмотрим задачу в стандартной форме с двумя переменными.
а11 X1 + a12X2 + … + а1nXn≤b1
а21 X1 + a22X2 + … + а2nXn≤b2
(4)………………………………….
am1 X1 + аm2X2 +…+ аmnxn ≤bm
(5) х1≥0, х2 ≥0
(6) F=C1x1+C2x2→max
Замечание: к такой форме может быть сведена КЗ, когда число переменных n, больше числа уравнений на 2, т.е. n – m = 2
Теорема 2.1:
Множество решений неравенства а11 X1 + a12X2 ≤b1, с двумя переменными является одной из полуплоскостей, на которые вся плоскость делится прямой, включая эту прямую (а11 X1 + a12X2 =b1), а другая полуплоскость с этой же прямой есть множество решений неравенства а11 X1 + a12X2 ≤b1
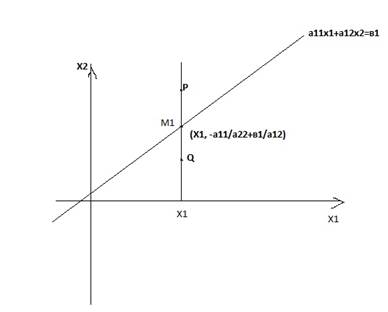
PQ║OX2,x2p 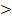 x2m и x2q
x2m и x2q 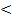 x2m↔х2
x2m↔х2 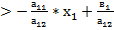 │*а12
│*а12 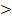 0
0
Замечание: n=3 (x1,x2,x3) – точка пространства (7) а11х1+а12х2+а13х3=b1 – плоскость
Решением неравенства а11х1+а12х2+а13х3 ≤ b1 будет одно из полупространств, на которые данная плоскость делит все пространства, включая эту плоскость.
Если 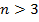 , то (x1,x2,…xn) – точка n-мерного пространства
, то (x1,x2,…xn) – точка n-мерного пространства
(8) а11 X1 + a12X2 + a13X3 + … + а1nXn = b1 – гиперплоскость
Теорема 2.2:
Множество всех решений линейного неравенства с «n» переменными
а11 X1 + a12X2 + a13X3 + … + а1nXn ≤ b1 является одним из полупространств, на которые все пространство делится гиперплоскостью (8), включая эту плоскость
Множество решений системы неравенств
2х1+х2≤3
х1+2х2≤3
х1≥0, х2≥0
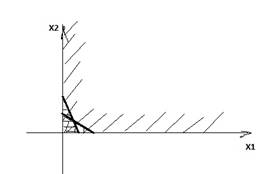
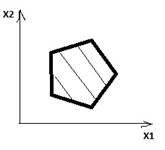
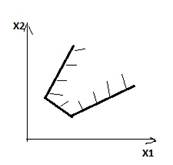
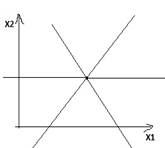
а)Ограниченное множество б)неограниченное множество в) точка
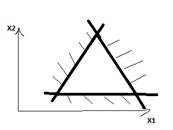
г)система несовместна (множество решений пусто)
Опр.1 Множество точек плоскости (пространства) называется выпуклым, если вместе с любыми двумя своими точками содержит весь отрезок, соединяющий эти точки.
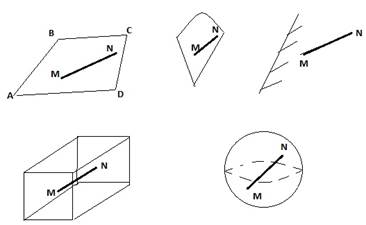
Теорема 2.3:
Пересечение выпуклых множеств – есть выпуклое множество
Доказательство:
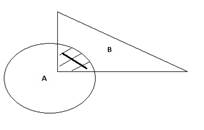 Пусть M и N
Пусть M и N 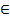 A
A 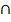 B, отсюда M и N
B, отсюда M и N 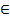 A; и M и N
A; и M и N 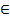 B (А и В выпуклые множества) следовательно MN
B (А и В выпуклые множества) следовательно MN 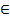 A и MN
A и MN 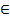 B, отсюда MN
B, отсюда MN 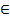 A
A 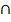 B
B
Следствие: множество решений системы неравенств (4) является выпуклым (если оно не пусто).
Опр2. Точка множества называется внутренней, если в некоторой ее окрестности содержатся только точки данного множества.(М)
Опр3. Точка множества называется граничной, если в любой ее окрестности содержатся, как точки данного множества, так и точки, не принадлежащие данному множеству.(N)
Опр4. Точка выпуклого множества называется угловой или крайней, если она не является внутренней ни для какого отрезка целиком принадлежащего данному множеству.(Р)
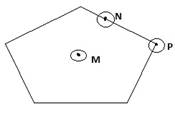
Опр5. Множество точек называется замкнутым, если оно содержит все свои граничные точки.
Опр6. Множество называется ограниченным, если существует круг (в пространстве шар) конечного радиуса, который полностью содержит в себе данное множество.
Опр7. Выпуклое замкнутое множество точек плоскости (пространства), имеющее конечное число угловых точек называется выпуклым многоугольником (многогранником), если оно ограничено и выпуклой многоугольной областью, если оно неограниченно.
Теорема 2.4:
Множество решений совместной системы (4), (5) m линейных неравенств с двумя переменными является выпуклым многоугольником (многоугольной областью).
Замечание: Опр.1-7 имеют место и в случае n-мерного пространства.
Х'=(x1', x2',…xn')
X2=(x12,x22,…xn2)
Отрезком, соединяющим эти точки, называется множество точек Х=(x1,x2,…xn), удовлетворяющих условию Х=αх'+(1-α)x2, где α 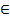 [0;1] можно переписать в виде Х=α1х1+α2x2, где α1,α2≥0, α1+α2=1
[0;1] можно переписать в виде Х=α1х1+α2x2, где α1,α2≥0, α1+α2=1
Опр. Точка Х называется выпуклой линейной комбинацией точек х1, х2,..хn, если Х=α1х1+α2x2+..+ αnxn
Теорема 2.5:
Множеством решений совместной системы m неравенств с n переменными является выпуклым многогранником (многогранная область) в n-мерном пространстве.
Теорема 2.6:
Выпуклый многогранник является выпуклой линейной комбинацией своих угловых точек.
Геометрическим способом можно решить только стандартную задачу (4) – (6) с двумя переменными (n=2).
F=C1x1+C2x2
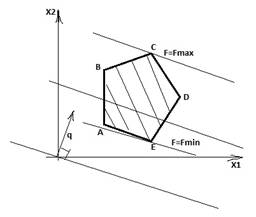
Линия уровня функции F=F(х1;х2)
F=a
C1x1+C2x2=а – прямая
gradF(x1;x2)=(z'x1;z'x2) – показывает направление наискорейшего роста функции.
q=gradF=(C1;C2)
min – в точке Е – точке входа в многоугольник
max – в точке С – точка выхода из многоугольника
Пример:
2х1+3х2≤12
2х1+х2≤8
х1≥0, х2≥0
F=4x1+3x2→max
1)2х1+3х2=12
2)2х1+х2=8
Линия уровня F=0
q=(4,3)
B – Точка пересечения прямых 1) и 2)
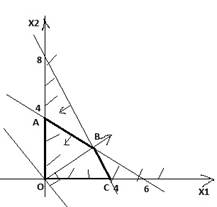
2х1+3х2=12
2х1+х2=8
х1=3;х2=2
Fmax=4*3+3*2=18
Замечание: При решении графическим методом задачи (4) – (6) на отыскание max возможны следующие случаи:
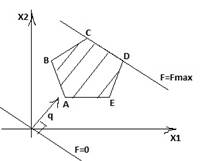
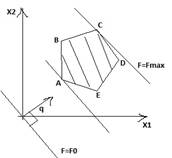
бесконечное множество оптимальных единственное оптимальное решение
решений CD=a i 1x1+a i 2x2=b i
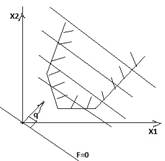
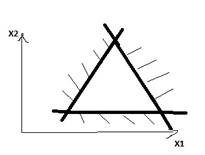
отсутствует конечный оптимум F=∞ отсутствие допустимых решений
Теорема 3.1:
Если ЗЛП имеет оптимальное решение, то линейная функция принимает max (min) значение в одной из угловых точек многогранника решений. Если функция принимает max(min) более чем в одной угловой точке, то она принимает его в любой точке, является выпуклой линейной комбинацией этих точек.
3. Метод исключения Жордано-Гаусса для систем линейных уравнений. (базовые, свободные переменные, разрешающий элемент, базисное решение, опорный план, вырожденное решение)
Данасистема: a11x1+a12X2+…+a1nxn = b 1
……………………………………………………………
am1x1+am2X2+…+amnxn= b ь
Замечание
Будем считать, что ранг А=m, т.е. все уравнения линейно независимы. Если rangA=m=n, то решение единственное. Если rangA=m<n- бесконечное кол-во решений.
Любые m-переменные системы называются базисными или основным, если определитель матрицы коэффициентов при них отличен от нуля, а остальные n-m переменные – свободные. |a11a1n |
|am1amn|
A= (a11…a1j…a1n|b1)
....
(ai1…aij….ain|bi )
....
(am1..amj…amn|bm)
Пусть aij не равно 0 – разрешающий элемент, ai1…aij….ain - разрешающая строка\ стобец
3. Метод исключения Жордано-Гаусса для систем линейных уравнений. (базовые, свободные переменные, разрешающий элемент, базисное решение, опорный план, вырожденное решение)
Данасистема: a11x1+a12X2+…+a1nxn = b 1
……………………………………………………………
am1x1+am2X2+…+amnxn= b ь
Замечание
Будем считать, что ранг А=m, т.е. все уравнения линейно независимы. Если rangA=m=n, то решение единственное. Если rangA=m<n- бесконечное кол-во решений.
Любые m-переменные системы называются базисными или основным, если определитель матрицы коэффициентов при них отличен от нуля, а остальные n-m переменные – свободные. |a11a1n |
|am1amn|
Алгоритм.
На первом этапе (прямой ход) система приводится к ступенчатому виду, путем последовательного исключения переменных.
На втором этапе решения (обратный ход) мы будем последовательно находить переменные из получившейся ступенчатой системы.
1. Выбирают первый слева столбец матрицы, в котором есть хоть одно отличное от нуля значение.
2. Если самое верхнее число в этом столбце ноль, то меняют всю первую строку матрицы с другой строкой матрицы, где в этой колонке нет нуля.
3. Все элементы первой строки делят на верхний элемент выбранного столбца.
4. Из оставшихся строк вычитают первую строку, умноженную на первый элемент соответствующей строки, с целью получить первым элементом каждой строки (кроме первой) ноль.
5. Далее проводят такую же процедуру с матрицей, получающейся из исходной матрицы после вычёркивания первой строки и первого столбца.
6. После повторения этой процедуры 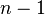 раз получают верхнюю треугольную матрицу
раз получают верхнюю треугольную матрицу
7. Вычитают из предпоследней строки последнюю строку, умноженную на соответствующий коэффициент, с тем, чтобы в предпоследней строке осталась только 1 на главной диагонали.
8. Повторяют предыдущий шаг для последующих строк. В итоге получают единичную матрицу и решение на месте свободного вектора (с ним необходимо проводить все те же преобразования).
9. Чтобы получить обратную матрицу, нужно применить все операции в том же порядке к единичной матрице.
Пример
Для решения следующей системы уравнений:
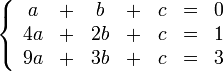
Запишем её в виде матрицы 3×4, где последний столбец является свободным членом:
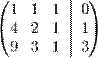
Проведём следующие действия:
· К строке 2 добавим: −4 × Строку 1.
· К строке 3 добавим: −9 × Строку 1.
Получим:
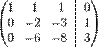
· К строке 3 добавим: −3 × Строку 2.
· Строку 2 делим на −2
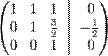
· К строке 1 добавим: −1 × Строку 3.
· К строке 2 добавим: −3/2 × Строку 3.
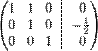
· К строке 1 добавим: −1 × Строку 2.
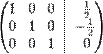
В правом столбце получаем решение:
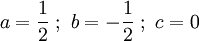 .
.
Через конечное число шагов получим таблицу, где m-столбцов, в которых, каждая из исключенных переменных входит в только одно из уравнений системы с коэф=1. Исключенные переменные являются базисными, а остальные – свободными. Конечная таблица –приведённая. Решение x=(x1, x2…xn) называется допустимым, если все его компоненты не отрицательные. Допустимое базисное решение называется опорным планом.
Базисное решение, в котором хотя бы одна неосновная базисная переменная равна нулю, называется вырожденное.
4. Симплексные преобразования исключения переменных
Симплексное преобразование определяется двумя особенностями. В качестве разрешающего столбца выбирается тот, где есть хотя бы один положительный элемент. В качестве симпл. разреш. Элемента выбирается тот положительный элемент, для которого в соответсв. строке отношение правой части системы к этому элементу является минимальным.
Замечание: Без огранич. общ.можно считать, что в системе все правые части не отрицательные. Если какое то bi<0, то соответствующее уравнение умножается на (-1).
Считаем, что bi>=0, то: В симплексных преобразованиях системы, в которых все переменные правой части не отрицательные, есть неотрицательное базисное решение. Если получено одно неотрицательное базисное решение, то остальные неотрицательные базисные решения можно получить из него симплексными преобразованиями.
Док-во из формул пересчета симплексных преобразований.
В самом деле не нулевые компоненты базисного решения равны правым частям βi, а они остаются неотрицательными.
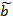 =
= 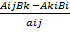 , где a – разрешающий элемент
, где a – разрешающий элемент
Если akj<0 то 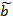 k>=0 /// если akj>0, то
k>=0 /// если akj>0, то 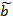 k делится на akj=> то
k делится на akj=> то 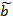 k>0
k>0
1) Составляем симплекс таблицу из коэффициента системы
2) Выбираем разрешающий элемент
3) Осуществляется пересчет по след.правилам:
1. все элементы делятся на разрешающий элемент.
2. все элементы разрешающего столбца зануляются.
3. пересчет по правилу прямоугольника.
Если в разрешающей строке имеется 0, то соответствующий столбец переносится без изменений.
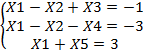
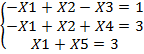
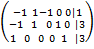 =
= 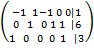 =….=
=….= 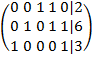 =
= 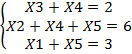
Базисное решение (0,1,0,2,3)
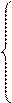 5.Решение симплексным методом, канонической задачи Л.П.
5.Решение симплексным методом, канонической задачи Л.П.
A11X1+A12X2+...A1nXn=B1
A21X1+A22X2+...A2nXn=B2 (12)
Am1X1+Am2X2+...AmnXn=Bm
X1,2>=0 Xn>=0 (13)
F=C1X1+C2X2+...CnXn-->max (14)
___
rang A=m Bj>=0 (i=1,m)
Тогда, с помощью симплексных преобразований системы(12), можно привести к виду:
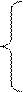 X1+d1.m+1Xm+1+...d1.nXn=B1
X1+d1.m+1Xm+1+...d1.nXn=B1
X2+d2.m+1Xm+1+...d2.nXn=B2 (15)
Xm+dm.m+1Xm+1+...dm.nXn=Bm
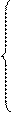
X1=-d1.m+1Xm+1+...-d1.nXn=B1
X2=-d2.m+1Xm+1+...-d2.nXn=B2 (15)
Xm=-dm.m+1Xm+1+...-dm.nXn=Bm
(15) - общее решение
Решение (B1,B2,Bm, 0,0) -допустимое базисное решение.
Подставляя в целевуюфун-ю (14) вместо базисных пер-ныч X1,X2,Xm их выражения (15)
через свободное, получим:
F=-jm+1Xm+1-jm+2Xm+2-...-jnXn+j (17)
Для получения базисного решения (16) значения целевой ф-ии F=j0
m
jn=d1кC1+d2кC2+...dmкCn-Cк= 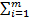 diкCi-Cк
diкCi-Cк
i=1
j0=B1C1+B2C2+...BnCn-C0
величина jn-оценки
Если все jnn>=0, то увеличить значения fun F нельзя и следовательно решения (16)является
оптимальным и Fmax=jo
F=-3X1-2X2+5
X1-0x2=0 Fmax=5
Если существует jp<0, то значения фун-ии можно увеличить за счет увеличения
соответствующей переменной Хр.
Пер-ю Хр нужно включить в базис, а одну из базисных пер-х перевести в свободное,
чтобы новое базисное было допустимым, при переходе к новому базису, нужно использовать
симплексные преобразования.
Все эти вычисления проводят в симплекс таблицах.
Перенесем ф-ию цели (17) в виде:
F+jm+1Xm+1+jm+2Xm+2..+jnXn=Jо и добавим это рав-во к сис-меогранич (15)
если Переменная F, входит только в одно ур-ние,то она всегда будет базисной
| Базис | X1 | X2 | Xm | Xn+1 | Xn | |
| X1 | d1.m+1 | d1n | B1 | |||
| X2 | d2.m+1 | d2n | B2 | |||
| Xm | dm.m+1 | dmn | Bm | |||
| F | jm+1 | jn | jo |
Cимплекс-таблица для нового опорного плана, получают симплпреобр-м данной табл, где в качестве
разреш столбца берут столбец соотв-й отрицательной оценке замещения.
Алгоритм:
1)проверяют выполнение критериев оптимальности при решение задачи на max-наличие в последней строке отриц. Коэффициентов ji<0 если все значения j≥0, то решение оптимально допустимо Fmax=j0
(В1,В2,Вm,0,0,0)-оптимреш
Если критерий оптимально не выполнен то выполняют симплекс преобразования переходя к новому опорному плану.
2)Выбирают разрешающий столбец для которого оценка замещения отрицательная и хотя бы один элемент из этого столбца положителен.Если таких столбцов несколько то выбирают столбец с наиб по модулю отрицательной оценкой.
3)Вычисляют оценочные отношения т.е. отношение элемента столбца свободных членов и соответственно положит. Элементам разреш столбца
4)строим следующее таблицу по следующим правилам
А)первоначальная Хрвводится в базис, а первоначальная Хq становится свободным
Б) все элементы разрешающей строки делятся на разрешающий элемент.
В)все элементы разрешающего столбца кроме разреш элемента зануляются
Г) все остальные элементы пересчитываются по правилу прямоугольника
Д)с полученной табл.повторяются пункты с 1-5
Теорема 8
Если после выполнеия очередной операции:
1) найдется хотя бы одна отриц. Оценка и в каждой таблице с такой оценкой окажется хотя бы один один положительный то можно можно улучшить решение
2)если найдется хотя бы одна отрицательная оценка, столбец который не содержит который не содержит положительных эл-ов, то функция не ограничена сверху в области доп решений т.е. не существует конечного max.
3)все оценки окажутся не отрицательными, ji≥0, то достигнуто оптимальное решение.
Транспортная задача. Постановка задачи. Закрытая и открытая ТЗ. Приведение открытой ТЗ к закрытой. Число положительных компонентов опорного плана.
Пусть некоторый однородный продукт имеется у m поставщиков А1,А 2…Аm. Его необходимо доставить n-потребителям В1, В 2….Вn
Известна стоимость Cijперевозки ед. груза.
Необходимо составить оптимальный план перевозок Xij
Пусть запасы и потребности сбалансированы 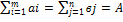
Составим матем. модель.
Общие транспортные расходы.
 F=
F= 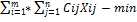
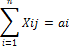
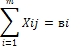
Дата добавления: 2015-08-20; просмотров: 195 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Кладка в зимнее время | | | Приведение открытой ТЗ к закрытой. |