Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Метод множителей Лагранжа. Построим функцию

Билет.метод потенциалов. | Вырожденность в транспортных задачах | Альтернативный оптимум в транспортных задачах | Целочисленное программирование. Метод Гомори (правильное отсечение, правила формирования правильного отсечения). | Пример. | Графический метод решения задачи целочисленного программирования. | Теорема 1.1 | Теорема 1.2 | Графический метод решения задач нелинейного программирования | Нелинейная целевая функция и линейная система ограничений. |


Читайте также:
  1. Case-метод Баркера
  2. I. Методические рекомендации по выполнению самостоятельной работы студентов.
  3. I. Организационно-методический раздел
  4. I. Понятие, формы и методы финансового контроля
  5. II. Материалы и методы
  6. II. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ СТУДЕНТОВ
  7. III. Источники и методы получения аудиторских доказательств при проверке кредитов и займов

Z =f(x1,x2 …xn)→max(min) (3)

gi (x1,x2 …xn)=0 (4) i=1,m

Построим функцию

L(x1,x2 …xn)=f(x1,x2 …xn)+∑Xigi (x1,x2 …xn) (5) – функция Лагранжа

λ1…λm

L(x)=f(x)+∑λigi(x))

Теорема3.1: Если точка Xo является точкой условного экстремума функции Z=f(x) при условии (4), то существуют такие значения λ1o,λ2o, что точка (x1o,x2o…xno,λ1o,λ2o…λmo) является точкой extrфункции Лагранжа(5), то есть задача сводиться к исследованию на локальный extr функции Лагранжа. Необходимые условия extrдля функции L(x, λ):

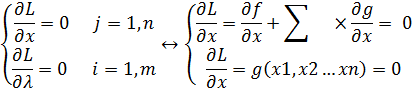
Решая эту систему находим точки (x1o, x2o…xno…λ1o), которые могут являться точками локального extrи следовательно точка Xo =(x1o,x2o … xno) – точка подозрительная на условный extr.

Пусть Z =f(x1,x2)→max(min) (6)

g(x1,x2)=0
Функция Лагранжа L=f(x1,x2)+λg(x1,x2)

Дата добавления: 2015-08-20; просмотров: 64 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Условный экстремум. Метод множителей Лагранжа| Условный экстремум функции двух переменных
mybiblioteka.su - 2015-2024 год. (0.007 сек.)