Симплекс-метод с естественным базисом

Для применения симплекс-метода с естественным базисом КЗЛП должна содержать единичную подматрицу размером mxm – в этом случае очевиден начальный опорный план (неотрицательное базисное решение системы ограничений КЗЛП).

Для определенности предположим, что первые m векторов матрицы системы уравнений составляют единичную матрицу. Тогда первоначальный опорный план очевиден – (b1, b2,…, bm,0,…,0).

Проверка на оптимальность опорного плана проходит с помощью признака оптимальности, переход к другому опорному плану проводится с помощью преобразований Жордана-Гаусса при использовании математического признака оптимальности. Полученный опорный план снова проверяется на оптимальность и так далее. Процесс заканчивается за конечное число шагов, причем на последнем шаге либо выявляется неразрешимость задачи (конечного оптимума нет), либо получается оптимальный опорный план и соответствующее ему оптимальное значение ЦФ.

Математический признак оптимальности состоит из следующих двух теорем:

1. Если для всех векторов А₁, А₂,…, А_n выполняется условие

где ,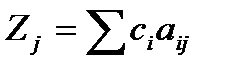

то полученный опорный план является оптимальным.

2. Если для некоторого вектора, не входящего в базис, выполняется условие 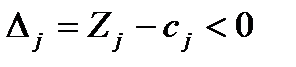, то можно получить новый опорный план, для которого значение ЦФ будет больше исходного, при этом могут быть два случая:

- если все компоненты вектора, подлежащего вводу в базис, неположительны, то ЗЛП не имеет решения (конечного оптимума нет);

- если имеется хотя бы одна положительная компонента у вектора, подлежащего вводу в базис, то можно получить новый опорный план.

На основании признака оптимальности в базис вводится вектор А_к , давший минимальную отрицательную величину симплекс разности: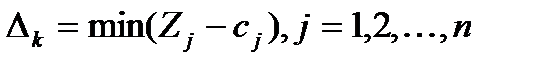

Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор А_r, который дает минимальное положительное оценочное отношение

Строка А_r называется направляющей, столбец А_к и элемент a_{r к} – направляющими.

Элементы направляющей строки в новой симплекс-таблице вычисляются по формулам:

а элементы i-й строки – по формулам: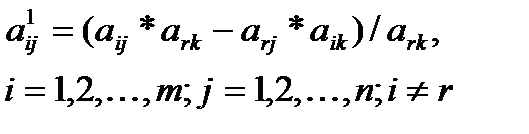

Значения нового опорного плана рассчитываются по формулам:

для i = r;

Процесс решения продолжают либо до получения оптимального плана, либо до установления неограниченности ЦФ. Если среди симплекс-разностей (оценок) оптимального плана нулевые только оценки, соответствующие базисным векторам, то это говорит о единственности оптимального плана. Если же нулевая оценка соответствует вектору, не входящему, то в общем случае это означает, что оптимальный план не единственный.

Примечание. Для использования приведенной процедуры к минимизации линейной функции f (x₁,x₂,…, x_n) следует искать максимум - f (x₁,x₂,…, x_n), затем полученный максимум взять с противоположным знаком. Оптимальное решение то же.

Пример. Получить решение по модели:

Эта задача (модель) линейного программирования, приведем ее к каноническому виду путем введения дополнительных переменных x 3 и x4:

КЗЛП имеет необходимое число единичных столбцов, т.е. обладает очевидным начальным опорным планом (0,0,300,150). Решение осуществляется симплекс-методом с естественным базисом с оформлением расчетов в симплекс-таблицах:

Номер			В
симплекс-	Базис		план		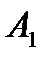			Q
таблицы
	А3
	А4
		f(x)		-2	-3
	А2			1/3		1/3
I	А4			2/3		-1/3
		f(x)		-1
	А2					1/2	-1/2
II	А1					-1/2	3/2
		f(x)				1/2	3/2

В симплекс-таблице II получен оптимальный опорный план, поскольку все симплекс-разности (оценки) j. Оптимальные значения переменных равны: x1*=75, x2* =75 (основные переменные), x3* =0, x4* =0 (дополнительные переменные). Максимальное значение целевой функции равно 375.

Таким образом, в рассмотренной выше задаче об оптимальном использовании ограниченных ресурсов, оптимальная производственная программа состоит в выпуске 75ед. изделий первого вида и 75ед. изделий второго вида. С этой программой связана максимальная выручка от реализации готовой продукции – 375 у.е.

Основные понятия теории двойственности

Каждой задаче линейного программирования соответствует другая задача, которая называется двойственной к ней. Вместе взятые, эти задачи образуют пару взаимно двойственных задач и любую из них можно рассматривать как исходную. Решая одну из этих задач, можно получить решение и другой задачи.

Экономико-математические модели и содержательные экономические интерпретации исходной и двойственной задач можно представить следующим образом (таблица1).

Таблица 1- Содержательные интерпретации двойственных задач

Задача 1 (исходная)

Задача II (двойственная)

Z = c1x1 + c2x2 +…+cnxn => max при ограничениях: a11x1 + а12x2 +…+ а1nxn < b1 a21x1 + a22x2 +…+ а2nxn < b2 ……………………………… am1x1 + аm2x2 +…+ аmnxn < bm   и условии неотрицательности: x1 ≥0, x2 ≥0,…, xn ≥0. Составить такой план выпуска продукции Х = (х1, х2, …, хn), при котором прибыль (выручка) от ее реализации будет максимальной при условии, что потребление ресурсов по каждому виду не превзойдет имеющихся запасов.

F = b1y1 + b2y2 +…+ bmym =>min при ограничениях: a11у1 + а21у2 +…+ аm1y1 ≥ c1 a12y1 + а22y2 +…+ аm2y2 ≥ c2 ……………………………… a1ny1 + а2ny2 +…+ аmnym ≥ cn   и условии неотрицательности: y1 ≥0, y2 ≥0, …, ym ≥ 0. Найти такой набор цен (оценок) ресурсов Y = (y1, y2, …, ym), при котором общие затраты на ресурсы будут минимальными при условии, что затраты на ресурсы при производве каждого вида продукции будут не менее прибыли (выручки) от реализации этой продукции.

Цены ресурсов y₁, y₂, …, y_m в экономической литературе называют: учетные, неявные, теневые. Смысл их состоит в том, что это условные, “ненастоящие” цены. В отличии от “внешних” цен с₁, с₂, …, с_n на продукцию, известных, как правило, до начала производства, цены ресурсов y₁, y₂, …, y_m являются внутренними, так как они определяются непосредственно в результате решения задачи, а не задаются извне. Поэтому их чаще называют оценками ресурсов.

Независимо от содержательной интерпретации экономических параметров, обе задачи обладают следующими свойствами:

1. В одной задаче ищут максимум целевой функции, в другой – минимум.

2. Коэффициенты при переменных в целевой функции одной задачи являются свободными членами системы ограничений в другой.

3. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче.

4. Каждая из задач задана в стандартной форме, причем в задаче максимизации все неравенства вида «<», а в задачах минимизации – все неравенства вида «≥».

5. Матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг к другу:

a₁₁ а₁₂ … а_1n

для задачи I А = a₂₁ а₂₂ … а_2n ,

_{………………………………}

a_m1 а_m2 … а_mn

a₁₁ а₂₁ … а_m1

для задачи II А^т = a₁₂ а₂₂ … а_m2

_{………………………………}

a_1n а_2n … а_mn

6. Каждому ограничению неравенства исходной задачи соответствует в двойственной задаче условие неотрицательности переменных.

7. Каждому ограничению вида равно исходной задачи соответствует переменная без ограничения на знак в двойственной задаче.

8. Неотрицательным переменным исходной задачи соответствуют ограничения неравенства в двойственной задаче.

9. Неограниченным по знаку переменным исходной задачи соответствуют ограничения вида равно двойственной задачи.

Две задачи I и II линейного программирования, обладающие указанными свойствами, называются симметричными взаимно двойственными задачами или просто двойственными задачами.

Составление двойственной задачи можно осуществить по следующему алгоритму.

1. Привести все неравенства системы ограничений исходной задачи к одному смыслу, т.е., если исходная задача решается на максимум, то все неравенства системы ограничений привести к виду «<», если на минимум – к виду «≥». Для этого неравенства, в которых данное требование не выполняется, умножить на -1.

2. Составить расширенную матрицу системы А₁, в которую включить матрицу коэффициентов при переменных А, столбец свободных членов системы ограничений и строку коэффициентов при переменных в целевой функции.

3. Найти матрицу А ^т _1, транспонированную к матрице А₁.

4. Сформулировать двойственную задачу на основании полученной матрицы А ^т₁ и условий неотрицательности и неограниченности по знаку переменных.

Пример 1. Построить двойственную задачу к исходной:

Z = x₁ + x₂ + x₃ => min

x₁ + 2x₂ + x₃ ≥ 9

2x₁ + x₃ ≥ 4

х₁ ≥ 0, х₂ ≥ 0, х₃ ≥ 0.

Последовательность решения задачи.

1. В исходной задаче целевая функция минимизируется, знаки всех неравенств «≥». Поэтому можно сразу приступить к построению двойственной задачи.

В исходной задаче целевая функция минимизируется, поэтому в двойственной она будет максимизироваться.

В исходной задаче все ограничения имеют вид «≥», поэтому в двойственной все ограничения будут иметь вид «<».

В исходной задаче два ограничения, поэтому в двойственной будет две переменных у₁ и у₂.

Объемы ограничений исходной задачи будут коэффициентами при переменных в целевой функции двойственной задачи.

Коэффициенты при переменных в целевой функции исходной задачи будут объемами ограничений двойственной задачи.

Оба ограничения исходной задачи имеют вид неравенства, поэтому на две переменные двойственной задачи будут наложены условие неотрицательности, т.е. у₁ ≥ 0, у₂ ≥ 0.

2. Составим расширенную матрицу системы:

1 2 1 9

A₁ = 2 0 1 4

…………..

1 1 1 Z

3. Найдем матрицу А^т₁, транспонированную к А₁.

1 2 1

2 0 1

А^т₁ = 1 1 1

---------------

9 4 F

4.Сформулируем двойственную задачу:

F = 9y₁ + 4y₂ => max

y₁ + 2y₂ < 1

2y₁ < 1

y₁ + y₂ < 1

. у₁ ≥ 0, у₂ ≥ 0.

Пример 2.. Построить двойственную задачу к исходной:

Z = -x₁ + 2x₂ => max

2х₁ - х₂ ≥ 1

-х₁ + 4х₂ < 24

х₁ - х₂ < 3

х₁ + х₂ ≥ 5

х₁ ≥ 0, х₂ ≥ 0.

Последовательность решения задачи.

1. Так как исходная задача решается на максимум, то приведем все неравенства системы ограничений к виду «<», для чего обе части первого и четвертого неравенства умножим на -1.

Получим :

-2 х₁ + х₂ < - 1

-х₁ + 4х₂ < 24

х₁ - х₂ < 3

-х₁ - х₂ < - 5

2. Составим расширенную матрицу системы.

-2 1 -1

-1 4 24

A₁ = 1 -1 3

-1 -1 -5

-----------------

-1 2 Z

3. Найдем матрицу А^т₁, транспонированную к А₁.

-2 -1 1 -1 -1

1 4 -1 -1 2

А^т₁ = --------------------------

-1 24 3 -5 F

4.Сформулируем двойственную задачу.

F = -у₁ + 24у₂ + 3у₃ - 5у₄ => min

-2у₁ - у₂ + у₃ - у₄ ≥ -1

у₁ + 4у₂ - у₃ - у₄ ≥ 2

у₁ ≥ 0, у₂ ≥ 0, у₃ ≥ 0, у₄ ≥ 0.

Пример 3. Построить двойственную задачу к исходной:

Z = x1 - 2x2 + x3 - x4 + x5 => min

х1 - 2х2 + х3 + 3х4 - 2х5 = 6

2х1 + 3х2 - 2х3 - х4 + х5 < 4

х1 + 3х3 - 4х5 ≥ 8

х₁ ≥ 0, х₃ ≥ 0, х₅ ≥ 0;

х₂ и х₄ не имеют ограничения знака.

Последовательность решения задачи.

1 Умножим второе неравенство системы на -1. Так как целевая функция исходной задачи минимизируется, то все ограничения задачи должны иметь знак >.

В исходной задаче число ограничений три, поэтому в двойственной будет три переменных у₁, у₂, у₃.

В исходной задаче пять переменных, поэтому в двойственной будет пять ограничений.

В исходной задаче на переменные х₁, х₃, х₅ наложены условия неотрицательности, поэтому в двойственной задаче первое, третье и пятое ограничения будут неравенствами.

В исходной задаче переменные х₂ и х₄ не имеют ограничения знака, поэтому в двойственной задаче второе и четвертое ограничения будут уравнениями.

Второе и третье ограничения исходной задачи – неравенства, поэтому на переменные у₂ и у₃ в двойственной задаче будет наложено условие неотрицательности: у₂ ≥ 0, у₃ ≥ 0.

Первое ограничение исходной задачи – уравнение, поэтому переменная у₁ в двойственной задаче – без ограничения знака.

2 Составим расширенную матрицу системы.

1 -2 1 3 -2 6

-2 -3 2 1 -1 -4

A₁ =1 0 3 0 -4 8

---------------------------------------

Z

3 Найдем матрицу А^т₁, транспонированную к А₁.

1 -2 1 1

-2 -3 0 -2

1 2 3 1

А^т₁ = 3 1 0 -1

-2 -1 -4 1

------------------------------

6 -4 8 F

4 Сформулируем двойственную задачу.

F = 6y₁ - 4y₂ + 8y₃ => max

y₁ - 2y₂ + y₃ < 1

-2y₁ - 3y₂ = -2

y₁ + 2y₂ + 3y₃ < 1

3y₁ + y₂ = -1

-2y₁ - y₂ - 4y₃ < 1

у₂ ≥ 0, у₃ ≥ 0; у₁ не имеет ограничения знака.

---

Дата добавления: 2015-08-20