Введение. Рекомендовано к изданию методической комиссией экономического факультета (протокол

Бакалавр

Уфа 2013

УДК 364

ББК 27

Рекомендовано к изданию методической комиссией экономического факультета (протокол №___ от «___» _____________ 2013 г.)

Составитель: ст.преподаватель Сагадеева Э. Ф.

.

Рецензент: к.с.н., доцент кафедры математики Гильманова Г. Х.

Ответственный за выпуск: зав. кафедрой статистики и информационных систем в экономике, к.э.н., доцент Аблеева А.М.

ОГЛАВЛЕНИЕ

Введение
1. Геометрическая интерпретация задач линейного программирования
2. Симплексный метод решения задачи линейного программирования
3. Основные понятия теории двойственности
4.Двойственный симплекс-метод
5. Симплексный метод с искусственным базисом
6. Целочисленное программирование. Метод Гомори
7. Дробно-линейное программирование
8. Задачи нелинейного программирования. Метод множителей Лагранжа
9. Задания для самостоятельной работы
10. Тестовые задания
11. Задания для выполнения расчетно-графической работы и контрольной работы заочников
12. Фонд контрольных вопросов
13. Билеты к экзамену
14. Библиографический список

Введение

Методы оптимальных решений – это раздел математики, который изучает теорию и методы поиска лучших вариантов планирования хозяйственной деятельности человека как на одном определенном предприятии, так и в некоторой отрасли или в отдельном регионе, или в целом государстве.

Лучшие варианты – это те, при которых достигается максимальная производительность труда, минимум себестоимости, максимальная прибыль, минимум использования ресурсов и т.д. С точки зрения математики – это класс оптимизационных задач. Основным инструментом при их решении является математическое моделирование. Математическая модель – это формальное описание изучаемого явления и «перевод» всех существующих сведений о нем на язык математики в виде уравнений, тождеств, неравенств. Если все эти соотношения линейные, то вся задача называется задачей линейного программирования (ЗЛП). Критерием эффективности этой модели является некоторая функция, которую называют целевой.

Сформулируем общую задачу линейного программирования.

Пусть дана система m линейных уравнений и неравенств с n переменными (система ограничений):

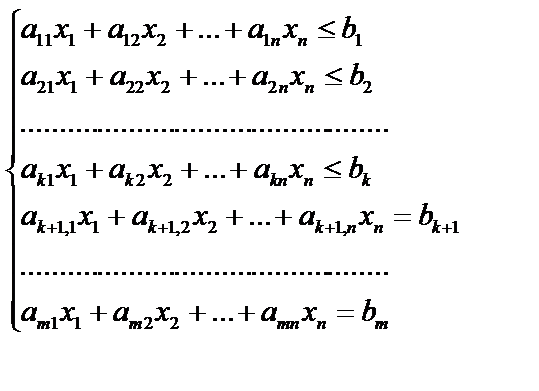(1)

и линейная функция

. (2)

Необходимо найти такое решение системы (1), при котором линейная функция принимает максимальное (минимальное) значение.

В общем случае ЗЛП может иметь бесконечное множество решений. Часто решение 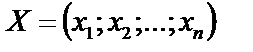, удовлетворяющее ограничениям (1), называют планом. Если все компоненты (3) для , то называют допустимым решением.

Оптимальным решением или оптимальным планом задачи линейного программирования называется такое ее решение 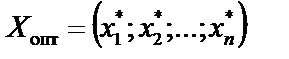, которое удовлетворяет всем ограничениям системы (1), условию (3) и при этом дает максимум (минимум) целевой функции (2).

Каноническая	Стандартная	Общая
1) Ограничения
Уравнения ,	Неравенства 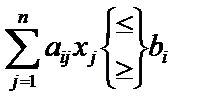,	Уравнения и неравенства ,
2) Условия неотрицательности
Все переменные ,	Все переменные 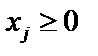,	Часть переменных , ,
3) Целевая функция
(max или min)

Здесь: 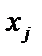– переменные задачи; 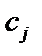– коэффициенты при переменных в целевой функции; 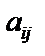– коэффициенты при переменных в основных ограничениях задачи; – правые части ограничений.

Линейное программирование - это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения. Таким образом, задачи линейного программирования относятся к задачам на условный экстремум функции. Казалось бы, что для исследования линейной функции многих переменных на условный экстремум достаточно применить хорошо разработанные методы математического анализа, однако невозможность их использования можно довольно просто проиллюстрировать.

Действительно, путь необходимо исследовать на экстремум линейную функцию

Z = С₁х₁+С₂х₂+... +С_Nx_N

при линейных ограничениях

a₁₁x₁ + a₂₂x₂ +... + a_1NХ_N = b₁

a₂₁x₁ + a₂₂x₂ +... + a_2NХ_N = b₂

...............

a_М1x₁ + a_М2x₂ +... + a_МNХ_N = b_М

Так как Z - линейная функция, то Z = С_j, (j = 1, 2,..., n), то все коэффициенты линейной функции не могут быть равны нулю, следовательно, внутри области, образованной системой ограничений, экстремальные точки не существуют. Они могут быть на границе области, но исследовать точки границы невозможно, поскольку частные производные являются константами.

Для решения задач линейного программирования потребовалось создание специальных методов. Особенно широкое распространение линейное программирование получило в экономике, так как исследование зависимостей между величинами, встречающимися во многих экономических задачах, приводит к линейной функции с линейными ограничениями, наложенными на неизвестные.

Дата добавления: 2015-08-20