Дробно-линейное программирование

Дробно-линейное программирование относится к нелинейному программированию, так как имеет целевую функцию, заданную в нелинейном виде.

Задача дробно-линейного программирования в общем виде записывается следующим образом:

при ограничениях

,

где с_j, d_j, b_i, a_ij – постоянные коэффициенты.

.

Рассмотрим задачу дробно-линейного программирования

при ограниченияхдробный линейный программирование

Будем считать, что .

Математическая модель задачи дробно-линейного программирования может быть использована для определения рентабельности затрат на производство изделий, рентабельности продаж, затрат в расчете на рубль выпускаемой продукции, себестоимости изделий.

Пример 1. Для производства двух видов изделий A и В предприятие использует три типа технологического оборудования. Каждое из изделий должно пройти обработку на каждом из типов оборудования. Известно время обработки каждого из изделий и затраты, связанные с производством одного изделия.

Тип оборудования	Затраты времени на обработку одного изделия, ч
А	В
I
II
III
Затраты на производство одного изделия, тыс. руб.

Оборудование I и III типов предприятие может использовать не более 26 ч и 39 ч соответственно, оборудование II типа целесообразно использовать не менее 4 ч.

Определить, сколько изделий каждого вида следует изготовить предприятию, чтобы средняя себестоимость одного изделия была минимальной.

Решение. Составим математическую модель задачи. Пусть х ₁ – количество изделий вида А, которое следует изготовить предприятию, х ₂ – количество изделий вида В. Общие затраты на их производство составят (2 х ₁+3 х ₂) тыс. руб., а средняя себестоимость одного изделия будет равна

.

Математическая модель задачи примет вид

при ограничениях

.

Задачу дробно-линейного программирования можно свести к задаче линейного программирования и решить симплексным методом.

Обозначим

при условии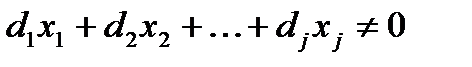

и введем новые переменные 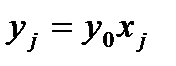. Тогда задача примет вид

при ограничениях

После нахождения оптимального решения полученной задачи, используя вышеуказанные соотношения, находят оптимальное решение исходной задачи дробно-линейного программирования.

Пример Решить задачу дробно-линейного программирования симплексным методом.

при ограничениях

.

Решение. Сведем данную задачу к задаче линейного программирования. Сначала введем дополнительные переменные, чтобы привести задачу к каноническому виду:

при ограничениях

.

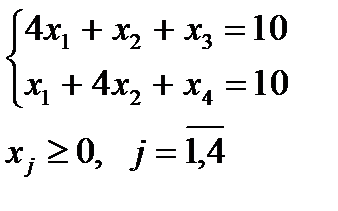Обозначим , , .

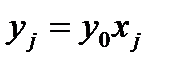Тогда задача принимает вид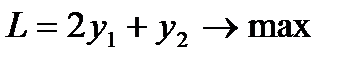

при ограничениях

.

Решим полученную задачу симплекс-методом. Введем дополнительную переменную, чтобы получить единичный базис:

при ограничениях

.

Составляем симплекс-таблицу.

Базис	План						z
		-10
		-10
z
L	-2 M	-8 M	-3 M -2	-2 M -1

В последней оценочной строке есть отрицательные оценки, поэтому нужно делать шаг симплекс-метода. Выбираем столбец с наименьшей оценкой, а затем разрешающий элемент – по наименьшему отношению свободных членов к коэффициентам столбца. Результат шага запишем в таблицу. Аналогично будем повторять шаги.

Базис	План						z
	5/2		31/4	7/2			5/4
	5/2		19/4	13/2			5/4
	1/4		3/8	1/4			1/8
L			-2	-1			M

Базис	План						z
	10/31			14/31	4/31		5/31
	30/31			135/31	-19/31		15/31
	4/31			5/62	-3/62		2/31
L	20/31			-3/31	8/31		M +10/31

Базис	План						z
	2/9				26/135	-14/135	1/9
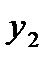
	2/9				-19/135	31/135	1/9
	1/92/3				-1/27	-1/54	1/18
L					11/45	1/45	M +1/3

Получили решение

, , , .

Тогда, возвращаясь к исходным переменным, получим:

, , .

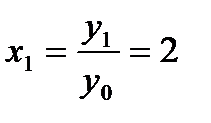Дата добавления: 2015-08-20