Читайте также:
|
при условиях:
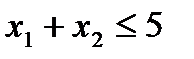
Решение. Запишем исходную задачу линейного программирования в форме основной задачи: найти максимум функции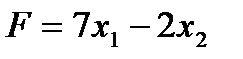 
при условиях
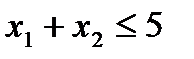
Составим для последней задачи двойственную задачу. Такой является задача, в результате решения которой требуется найти минимальное значение функции
Строим симплекс таблицу:
Итерация 0:
| Базис | 
| 
| 
| 
| 
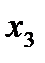
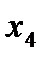
| Решение | Оценка |
| -7 | ||||||
 
| 
| ||||||
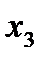
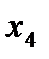
| -3 | ||||||
| -3 | -1 | - |
Условие допустимости выполняется, так как в графе «Решение» все значения положительные, но не выполняется условие оптимальности, так как -строка содержит отрицательный коэффициент. Продолжаем наши действия
Итерация 1:
| Базис |
|
|
|
|
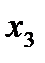
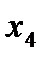
| Решение |
|
| ||||||
|
| ||||||
|
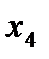
| -5 | -2 | -4 | |||
|
|
Данная симплекс-таблица не удовлетворяет условию допустимости, так как графа «Решение» содержит отрицательные значения, но удовлетворяет условию оптимальности, так как -строка не содержит отрицательных коэффициентов.
Итерация 2:
| Базис |
|
|
|
|
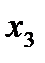
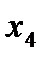
| Решение |
|
| 
| 
| 
| |||
|
| 
| 
| 
| |||
|
| 
| 
| 
| |||
|
| 
|
| 
|
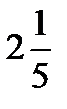
Полученная симплекс-таблица удовлетворяет и условию оптимальности и условию допустимости, так как она, во-первых, не содержит отрицательных коэффициентов в -строке, а, во-вторых, в графе «Решение» все значения положительные.
Таким образом, мы получили оптимальное, допустимое решение, которое имеет вид:
, 
Дата добавления: 2015-08-20; просмотров: 73 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Двойственный симплекс-метод | | | Симплексный метод с искусственным базисом |