Читайте также:
|
Рассмотрим частный случай общей задачи нелинейного программирования (11), (12), предполагая, что система ограничений (12) содержит только уравнения, отсутствуют условия неотрицательности переменных и 
и 
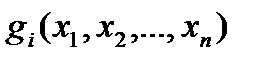- функции непрерывные вместе со своими частными производными
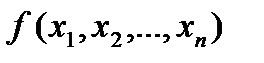® max (min) (14)
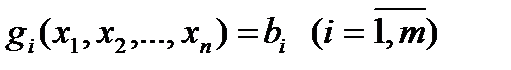(15)
Данную задачу называют задачей на условный экстремум или классической задачей оптимизации.
Чтобы найти решение этой задачи, вводят набор переменных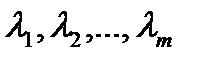 
называемых множителями Лагранжа, составляют функцию Лагранжа
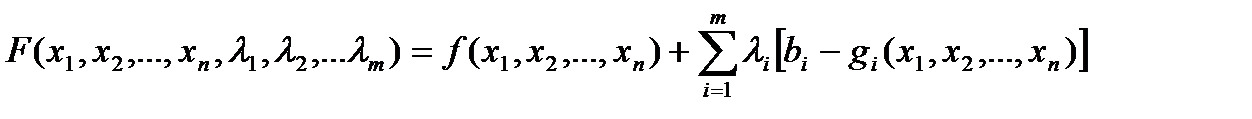(16)
находят частные производные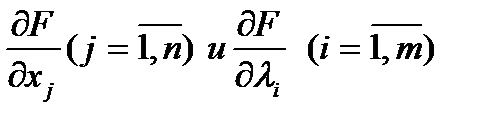 
и рассматривают систему n+m уравнений
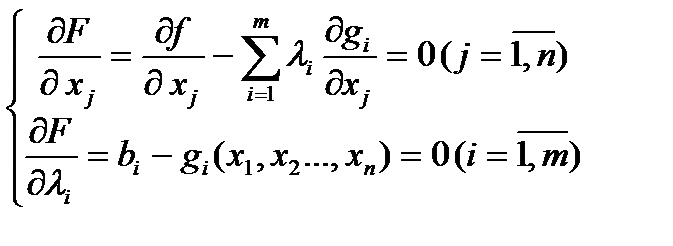(17)
с n+m неизвестными 
Всякое решение системы уравнений (17) определяет точку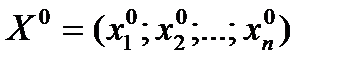 
в которой может иметь место экстремум функции 
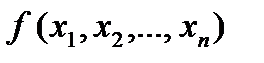. Следовательно решив систему уравнений (17), получают все точки, в которых функция (14) может иметь экстремальные значения.
Дата добавления: 2015-08-20; просмотров: 66 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задачи нелинейного программирования. Метод множителей Лагранжа | | | Алгоритм метода множителей Лагранжа |