Читайте также:
|
Этап 1. Составляют расширенную задачу (4) – (6).
Этап 2. Находят опорный план расширенной задачи.
Этап 3. С помощью обычных вычислений симплексного метода исключают искусственные векторы из базиса. В результате либо находят опорный план исходной задачи (1)- (3), либо устанавливают ее неразрешимость.
Этап 4. Используя найденный опорный план задачи (1) - (3), находят симплексным методом оптимальный план исходной задачи, либо устанавливают ее неразрешимость.
Задача 2. Найти максимум функции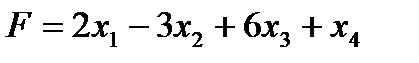 
при условиях
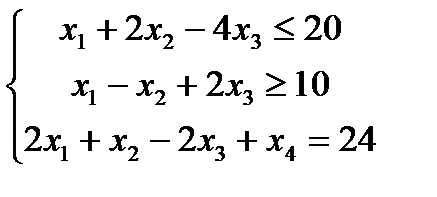
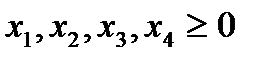
Этап 1. Составляем расширенную задачу к исходной, т.е. найти максимум функции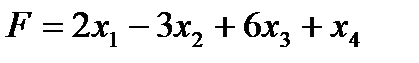 
при условиях
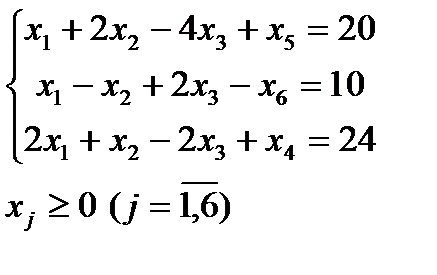
Среди векторов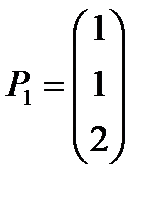 
, 
, 
, 
, 
, 
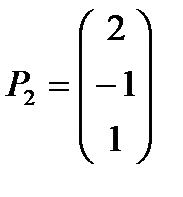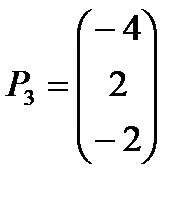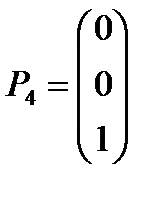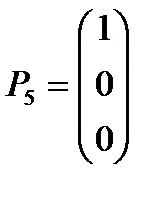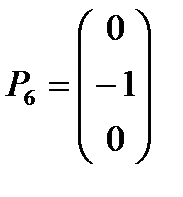имеется два единичных вектора 
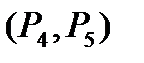, поэтому находим решение расширенной задачи состоящей в определении максимального значения функции
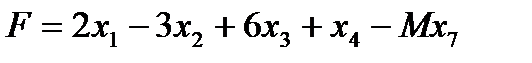при условиях
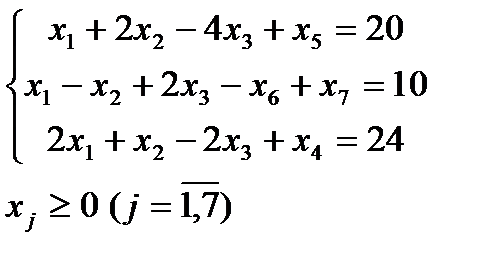
Этап 2. Опорный план имеет вид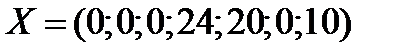 
, определяемый системой трех единичных векторов 
.
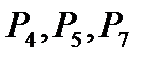Этап 3. Составляем таблицу для первой итерации
| i | Базис | Сб | Р 0 | -3 | - М | |||||
| Р 1 | Р 2 | Р 3 | Р 4 | Р 5 | Р 6 | Р 7 | ||||
| х 5 | -4 | |||||||||
| 2 | х 7 | -М | -1 | /2/ | -1 | |||||
| х 4 | -2 | |||||||||
| -8 | ||||||||||
| -10 | -1 | -2 |
Составляем таблицу для 2-ой итерации. Эта таблица содержит только четыре строки, так как искусственный вектор Р 7 из базиса исключен.
Этап 4.
| i | Базис | Сб | Р 0 | -3 | |||||
| Р 1 | Р 2 | Р 3 | Р 4 | Р 5 | Р 6 | ||||
| х 5 | -2 | ||||||||
| х 3 | ½ | -1/2 | -1/2 | ||||||
| х 4 | -1 | ||||||||
| -4 |
Из таблицы видно, что найденный опорный план исходной задачи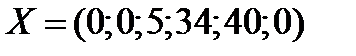 
не является оптимальным, поскольку в 4-ой строке столбца Р 6 этой таблицы находится отрицательное число (-4). Так как в указанном столбце нет положительных элементов (Теорема 2), то данная задача не имеет оптимального плана.
Дата добавления: 2015-08-20; просмотров: 173 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Пример. Найти максимальное значение функции | | | Целочисленное программирование. Метод Гомори. |