Читайте также:
|
Этап 1. Составляем функцию Лагранжа.
Этап 2. Находим частные производные от функции Лагранжа по переменным 
и приравниваем их нулю.
Этап 3. Решаем систему уравнений (17), находим точки, в которых целевая функция задачи может иметь экстремум.
Этап 4. Среди точек, подозрительных на экстремум, находим такие, в которых достигается экстремум, и вычисляем значения функции (17) в этих точках.
Задача 2. По плану производства продукции предприятию необходимо изготовить 180 изделий. Эти изделия могут быть изготовлены двумя технологическими способами. При производстве 
изделий 1 способом затраты равны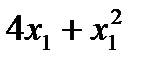 
руб., а при изготовлении 
изделий 2 способом они составляют 
руб.. Определить сколько изделий каждым из способов следует изготовить, чтобы затраты на производство продукции были минимальными.
Целевая функция для поставленной задачи имеет вид
® min при условиях 
.
Этап 1. Составляем функцию Лагранжа
.
Этап 2. Вычисляем частные производные по 
и приравниваем их нулю:
Этап 3. Решая полученную систему уравнений, находим 
Этап 4. Сделав замену в целевой функции 
, получим функцию от одной переменной, а именно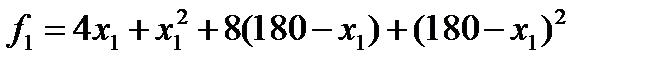 
Вычисляем 
или 
, откуда имеем 
. Значение целевой функции равно 17278 руб
Дата добавления: 2015-08-20; просмотров: 163 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Метод множителей Лагранжа | | | Задания для самостоятельной работы |