Автономные импульсные процессы. Алгоритм вычисления вектора импульсов и вершин.

Импульсные процессы

Для более глубокого анализа модели, имеющей вид взвешенного орграфа, необходимо принять некоторые весьма специальные допущения о влиянии изменений значения параметра одной вершины на параметры других вершин. Мы будем называть такие допущения правилами изменения значений параметров вершин. Выбор определенного правила играет весьма важную роль по отношению к нашим заключениям. Если допустить, что основ­ные данные (скажем, начальные значения параметров в каждой вершине и веса) известны лишь неточно, то окончательные выводы, основанные на определенном правиле изменения значений параметров вершин, будут также всегда неточными. Всякий полученный результат следует рассматривать как предварительный и он должен быть подвергнут "анализу чувствительности". Такой анализ будет включать повторное моделирование с измененными основными данными и, возможно, использование других правил изменения значений параметров вершин

Чтобы определить правило изменения значений параметров вершин, которое мы в дальнейшем примем, рассмотрим сначала знаковый орграф. Как обычно, его вершины представлены совокупностью ui, и2,..., ип. Предполагается, что каждая вершина ui принимает значение vi(t) в дискретные моменты времени t = 0,1,2,... Будем считать сначала, что значение vi(t+1) определяется значением vi(t) и информацией о том увеличили или уменьшили свои значения другие вершины uj, смежные с ui в момент времени t.

Если дуга из uj в ui положительна (отрицательна), то изменение в uj в момент t учитывается со знаком плюс (со знаком минус) в ui в момент t+1. Мы будем считать, что единичное изменение в uj влечет единичное изменение в ui. Таким образом, если дуга (uj, ui) положительна и pj(t) ‑ число, выражающее изменение в uj в момент t, то влияние на ui в момент t+1 изменения в иj увеличивает ui на величину рj(t). Если же дуга (uj, ui) отрицательна, то воздействие на ui в момент t+1 изменения в uj уменьшает ui на величину рj(t). Конечно, если рj(t). ‑ отрицательное число, то увеличение на рj(t). единиц означает уменьшение, а уменьшение на рj(t). единиц ‑ увеличение. Изменение рj(t)., называемое импульсом, задается разностью vj(t) ‑ vj(t ‑ 1) при t > 0. Необходимо указать и начальное условие при t =0. Подводя итоги, введем следующее обозначение:

Тогда для t >= 0 определим

vj(t + 1) = vi(t) + 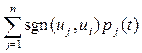(4)

Автономный импульсный процесс в знаковом орграфе D определяется по правилу (4) с вектором начальных значений

V(0)= (v1(0), v2(0),..., vn(0))

и вектором

P(0)= (p1(0), p2(0),..., pn(0)),задающим внешний импульс pj(0), вводимый в каждую вершину иj в момент времени 0. Мы будем также использовать вектор значений

V(t)= (v1(t), v2(t),..., vn(t))

и вектор импульсов

P(t)= (p1(t), p2(t),..., pn(t)).

Рассматривая автономный импульсный процесс, мы следим за распространением в системе начальных импульсов.

При анализе автономных импульсных процессов вектор начальных значений V(0) обычно определяется следующим образом. Предположим, что известно исходное значение vi(исх) в каждой вершине ui.Тогда vi(0) будет определяться соотношением

vi(0) = vi(исх)+рi(0),

т.е. vi (0) составлено из исходного значения и начального импульса вершины i. В дальнейшем чаще будем определять автономный импульсный процесс, задавая вектор

V(исх) = (v1 (исх), v2 (исх), … vn(исх)), а не вектор V(0).

В качестве примера использования автономного импульсного процесса рассмотрим знаковый орграф, изображенный на рис. 4.24, и примем, что Р(0) = (1, 0, 0, 0), а V(исх) = (0, 0, 0, 0). Таким образом, V(0) = (1, 0, 0, 0). В этом импульсном процессе единичный начальный импульс вводится в вершину 1. В момент t = 0 вершина и1 увеличивает значение на единицу; поэтому в момент t= 1 вершины и2 и u3 изменяются: вершина и2 увеличивает значение на 1, вершина и3 уменьшает значение на 1. Таким образом, V(l) = (1, 1, ‑1, 0) и поэтому Р(1) = (0, 1, ‑ 1, 0). Поскольку в момент времени t = 1 вершина u2 достигла значения 1, это приводит к увеличению на единицу значения вершины и4, в момент t= 2. Но вершина uз уменьшила на 1 свое значение в момент t = 1, что приводит (так как дуга (uз. и4) отрицательна) к последующему увеличению и4 на единицу в момент времени t=2. Мы заключаем, что V(2) =(1, 1, -1- 2) и Р(2)= (0, 0, 0, 2). Увеличение в u4 а две единицы в момент времени t = 2 приводит в свою очередь к увеличению на две единицы значения вершины u1 момент времени t =3. Итак, V(3) = (3, 1, ‑, 2). Этот процесс можно продолжить и далее. (Здесь ограничимся автономными импульсными процессами, которые рассматривались до сих пор. В более общей ситуации импульсный процесс может подвергаться воздействию внешних импульсов в любой момент времени.

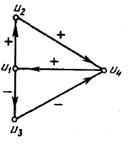
Рис. 1. Знаковый орграф

В этом случае полагаем, что 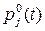представляет внешний импульс или изменение в вершине ui в момент t. Величина 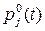должна добавляться к значению вершины ui в момент t. Таким образом, получаем более общую формулу для импульсного процесса

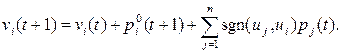(5)

В качестве начальных условий следует задать значения 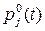для всех j и t, т.е. необходима та же информация, что и в обычном случае. Как правило, полагают .

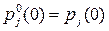Условие (4) для автономного импульсного процесса в знаковом оргра­фе естественным образом обобщается в правило изменения значений для автономного импульсного процесса во взвешенном орграфе. Мы просто полагаем

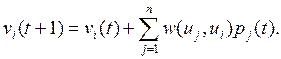(6)

где, как обычно, w(u, v) = 0, если дуга (и, v) отсутствует. Теперь, если имеется дуга из uj в uj с весом w = w(uj,uj) и значение вершины uj возрастает в момент времени t на к единиц, то в результате значение вершины uj в момент времени t + 1 возрастает на к * w единиц.

Поскольку vi(t + 1) ‑ vi(t) =pi(t + 1), уравнение (6) можно переписать в следующем виде:

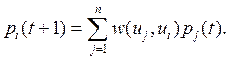(7)

(Это означает, что уравнения (6) действительно представляют систему конечно-разностных уравнений с параметрами w(uj,ui). Читателю следует также обратить внимание, что

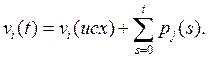(8)

мы ввели некоторое конкретное правило (закон) изменения значений, задаваемое уравнением (6). В нем безусловно пренебрегается временными запаздываниями и считается, что каждое воздействие происходит за единичное время. Как мы заметили ранее, если все временные сдвиги целочисленны, то их можно учесть, располагая между двумя вершинами, соединенными некоторой дугой орграфа, ряд новых вершин, соответствующих запаздыванию. И тогда можно анализировать импульсный процесс согласно введенному правилу. Недостаток этого подхода состоит в том, что получающиеся орграфы могут оказаться очень большими.

Дата добавления: 2015-08-17