Задачи нелинейного программирования. Метод множителей Лагранжа

Во многих экономических моделях исследования операций зависимости между постоянными и переменными факторами лишь в первом приближении можно считать линейными, более детальное рассмотрение позволяет обнаружить их нелиней­ность. Как правило, такие показатели, как прибыль, себестои­мость, капитальные затраты на производство и др., в действи­тельности зависят от объема производства, расхода ресурсов и т.п. нелинейно. В этом случае возникает задача нелинейного программирования, математическая модель которой имеет вид:

поиск переменных 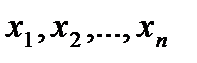удовлетворяющих системе неравенств (уравнений)

(1^/)

и обращающие в максимум (или минимум) целевую функцию, т.е.

(2^/)

(условия неотрицательности переменных, если они есть, входят в ограничения (1^/))

Можно выделить класс нелинейных задач, которые относятся к классическим методам оптимизации. Допустим, что среди огра­ничений (1^/) нет неравенств, не обязательны условия неотрица­тельности, переменные не являются дискретными, , а функ­ции и непрерывны и имеют частные производные по крайней мере второго порядка. В этом случае задачу оптимизации можно сформулировать так: найти переменные 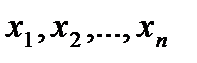удов­летворяющие системе уравнений

(1)

и обращающие в максимум (минимум) целевую функцию

(2)

Такие задачи в принципе можно решать классическими мето­дами дифференциального исчисления. Однако на этом пути встречаются такие вычислительные трудности, которые делают необходимым поиск других методов решения. Поэтому классические методы часто используется не в качестве вычислительного средства, а как основа для теоретиче­ского анализа.

Примером типичной и простой нелинейной задачи является следующая: данное предприятие для производства какого-то продукта расходует два средства в количестве х ₁ и х ₂ соответст­венно. Это факторы производства, например, машины и труд, два различных вида сырья и т.п., а величины х ₁ и х ₂ — затраты факторов производства. Факторы производства впредь будем считать взаимозаменяемыми. Если это "труд" и "машины", то можно применять такие методы производства, при которых величина затрат машин в сопоставлении с величиной затрат труда оказывается больше или меньше (производство более или менее трудоемкое). В сельском хозяйстве взаимозаменяе­мыми факторами могут быть посевные площади или мине­ральные удобрения (экстенсивный или интенсивный метод производства).

Объем производства (выраженный в натуральных или стои­мостных единицах) является функцией затрат производства .Эта зависимость называется производственной функ­цией. Издержки зависят от расхода обоих факторов и от цен этих факторов (c ₁и с ₂). Совокупные издержки выражаются формулой . Требуется при данных совокупных из­держках определить такое количество факторов производства, которое максимизирует объем продукции z.

Математическая модель этой задачи имеет вид: определить та­кие переменные удовлетворяющие условиям

(3)

при которых функция

(4)

достигает максимума.

Как правило, функция (4) может иметь произвольный не­линейный вид.

Используя классические методы оптимизации, следует четко представлять себе различие между локальным экстремумом функции, глобальным экстремумом и условным экстремумом. При этом полезно повторить определение локального и глобального экс­тремумов для функции одной переменной. Понятие условного экстремума вводится для случая, когда число переменных n не меньше 2 ().

Будем полагать, что функция 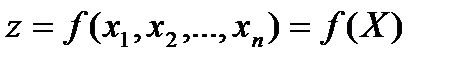дваж­ды дифференцируема в точке и в некоторой ее окрестности. Если для всех точек X этой окрестно­сти или , то говорят, что функция

f (X) имеет экстремум в X * (соответственно максимум или мини­мум).

Точка X *, в которой все частные производные функции z = f (X) равны 0, называется стационарной точкой.

Необходимое условие экстремума. Если в точке X * функция z = f (X) имеет экстремум, то частные производные функции в этой точке раны нулю:

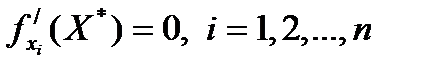
Следовательно, точки экстремума функции z = f (X) удовле­творяют системе уравнений:

(5)

Как и в случае одной переменной, необходимое условие не яв­ляется достаточным для того, чтобы стационарная точка была точ­кой экстремума. Для получения достаточных условий следует опре­делить в стационарной точке знак дифференциала второго порядка. Дифференциал второго порядка обозначается 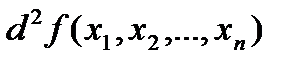и равен сумме произведений частных производных второго порядка на соответствующие приращения аргументов. Если от частной производной найти частную производную по переменной , то получим частную производную второго порядка по переменным , которая обозначается . В этом случае

Достаточные условия экстремума:

а) в стационарной точке Х ⁰ функция z = f { X) имеет максимум, 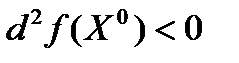, и минимум, если , при любых и (в этих случаях Х ⁰ = X *), не обращающихся в нуль одновременно;

б) если может принимать в зависимости от и и положительные, и отрицательные значения, то в точке Х ⁰ экс­тремума нет;

в) если может обращаться в нуль не только при нуле­вых приращениях и , то вопрос об экстремуме остается открытым.

Для функции двух переменных достаточные усло­вия еще не очень сложны. Существуют четыре частные производные второго порядка: Из них смешанные производные , если непрерывны, то равны.

Найдем значение частных производных второго порядка в ста­ционарной точке

(можно убедиться, что ). Обозначим через Δ определи­тель, составленный из для

Тогда достаточные условия экстремума функции двух переменных имеют вид:

а) если Δ > 0 и < 0 (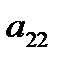 < 0), то в точке Х ⁰ функция имеет максимум: если Δ > 0 и > О ( > 0), то в точке Х ⁰ — минимум (в этих случаях Х ⁰ = X *);

б) если Δ < 0, то экстремума нет;

в) если Δ = 0, то вопрос об экстремуме остается открытым.
Схема определения экстремума функции n переменных совпадает с правилами определения локального экстремума функции одной переменной.

Задача 1. Исследовать на экстремум функцию

Решение. Находим частные производные:

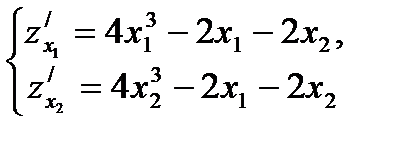(6)

Приравниваем частные производные нулю:

(7)

Решаем систему уравнений (7). Вычитая из первого уравне­ния второе, получим поэтому х ₁ = х ₂, и из первого уравнения найдем откуда x ₁= 0 или х ₁= = ±1.

Имеем три стационарные точки:

Найдем вторые частные производные, используя (6):

Вычисляем значения вторых частных производных в каждой стационарной точке, составляем определитель Δ и применяем достаточные условия экстремума.

В точке X ¹ = (0; 0) а ₁₁=-2; а ₁₂= а ₂₁= -2; а ₂₂=-2

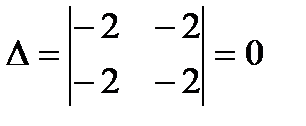
Вопрос об экстремуме остается открытым (такая точка называется седловой).

В точке X ² = (1; 1) (а также и в точке X ³ = (-1;-1)): а ₁₁=10; а ₁₂= а ₂₁= -2; а ₂₂=10

Функция в этих точках имеет минимум, так как Δ > 0, а ₁₁ > 0 Z _min= -2¹

Выше шла речь о локальном экстремуме функции n переменных. Как правило, в практических задачах необходимо определить наибольшее и наименьшее значения функции (глобальный экстремум) в некоторой области.

Говорят, что функция z = f { X) имеет в точке Х ⁰ заданной в области D глобальный максимум (наибольшее значение) или глобальный минимум (наименьшее значение), если неравенство f (X) ≤ f (X ⁰) или f (X) ≥ f (X ⁰) соответственно выполняется для любой точки X є D.

Если область D замкнута и ограничена, то дифференцируемая функция z = f (X) достигает в этой области своих наибольшего и наименьшего значений или в стационарной точке, или в граничной точке области (теорема Вейерштрасса).

Следовательно, чтобы найти наибольшее (наименьшее) значение функции z = f (X) в области D нужно:

1) найти все стационарные точки внутри области D и вычислить значения функции в них;

2) исследовать функцию на экстремум на границе области D;

3) сравнить значения функции, полученные в п. 1 и 2: наибольшее (наименьшее) из этих чисел и будет наибольшим (наименьшим) значением функции во всей области.

Граница области D аналитически может быть задана системой уравнений (условий) относительно переменных 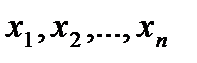По­этому, исследуя экстремальные свойства функции на границе, необходимо решить задачу определения условного экстремума.

Условный экстремум. Пусть необходимо найти экстремум функции z = f (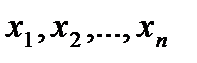) при условии, что переменные 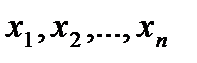удовлетворяют, уравнениям

(8)

Предполагается, что функции f и φ _i, имеют непрерывные част­ные производные по всем переменным. Уравнения (8) называ­ют уравнениями связи.

Говорят, что в точке Х ⁰ = (), удовлетворяющей уравнениям связи (8), функция z = f { X) имеет условный мак­симум (минимум), если неравенство ( 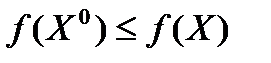f(X°) > f(X) (f(X°) < f{X)) имеет место для всех точек X, координаты которых удовлетворяют уравнениям связи.

Легко заметить, что задача определения условного экстремума совпадает с задачей нелинейного программирования (1), (2).

Один из способов определения условного экстремума приме­няется в том случае, если из уравнений связи (8) m перемен­ных, например , можно явно выразить через оставшиеся n-m переменных:

(9)

Подставив полученные выражения для x_i в функцию z, полу­чим

или

(10)

Задача сведена к нахождению локального (глобального) экс­тремума для функции (10) от n-m переменных. Если в точке функция (10) имеет экстремум, то в точке функция 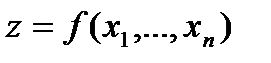имеет условный экстремум.

Итак, в общем виде задача нелинейного программирования состоит в определении максимального (минимального) значения функции

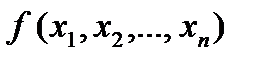(11)

при условии, что ее переменные удовлетворяют соотношениям

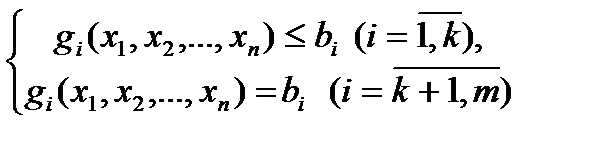(12)

где некоторые известные функции n переменных, а - заданные числа.

Здесь имеется в виду, что в результате решения задачи будет определена точка , координаты которой удовлетворяют соотношениям (12) и такая, что для всякой другой точки удовлетворяющей условиям (12), выполняется неравенство

(13)

Если линейные функции, то задача (11)- (12) является задачей линейного программирования.

Соотношения (12) образуют систему ограничений и включают в себя условия неотрицательности переменных, если такие условия имеются. Условия неотрицательности переменных могут быть заданы и непосредственно.

Дата добавления: 2015-08-20