Симплекс-метод решения задачи с искусственным базисом (М-метод).

Метод искусственного базиса применяется для решения ЗЛП симплекс-методом, в случае когда задача не имеет начального опорного решения с базисом из единичных векторов.

Согласно данному методу для ЗЛП составляется расширенная задача. На её основе находится или оптимальное решение исходной задачи, или устанавливается причина её отсутствия. В расширенной задаче используют искусственные переменные -неотрицательные переменные, которые вводятся в ограничения-равенства для получения начального опорного решения с базисом у единичных векторов. Каждая искусственная переменная вводится в левую часть одного из уравнений системы ограничений с коэффициентом +1, в целевую функцию в задаче на максимум с коэффициентом –М, на минимум +М.

1) Если расширенная ЗЛП имеет оптимальное решение, у которого все искусственные переменные равны 0, то исходная задача имеет оптимальное решение, которое получается отбрасыванием нулевых искусственных переменных.

2) Если расширенная ЗЛП имеет оптимальное решение, у которого хотя бы одна искусственная переменная отлична от 0, то исходная задача не имеет решения.

3) Если расширенная ЗЛП не имеет решения ввиду неограниченности целевой функции, то исходная задача не имеет решения.

32. Содержательная постановка транспортной задачи линейного программи­рования.

Транспортная задача является важным частным случаем распределительных ЗЛП.

Постановка транспортных задач состоит в определении оптимального плана перевозок, некоторого однородного груза из m пунктов отправления (от m поставщиков) А₁, А₂…Аm в n пункты назначения (n потребителям) В₁, В₂…Вn. При этом в качестве критерия оптимальности взята минимальная стоимость перевозок всего груза.

Введём обозначения:

c_ij -тариф перевозки единицы груза из пункта отправления A_i в пункт назначения Bj

- запас груза в пункте отправления A_i

- потребность в грузе в пункте назначения Bj

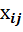- количество единиц груза перевозимого из пункта отправления А в В.

Математической моделью транспортной задачи будет задача определения минимального значения целевой функции F.

→min

при ограничениях:

Дата добавления: 2015-08-20