Читайте также:
|
Определение1:
Задача 
→min, 
является транспортной ЗЛП.
Определение2:
Всякое базисное решение соотношений, 
называется планом транспортной ЗЛП или планом перевозок.
Определение3:
Всякое базисное решение соотношений называется опорным планом транспортной ЗЛП.
Определение4: План Х=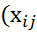 
) при котором целевая функция достигает своего минимального значения, называется оптимальным планом транспортной задачи.
Определение5: Если общая потребность в грузе в пунктах отправления равна суммарному запасу груза в пунктах отправления, то модель транспортной задачи называется закрытой.
В случае, если соотношения не выполняются, то модель называется открытой.
Дата добавления: 2015-08-20; просмотров: 43 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Симплекс-метод решения задачи с искусственным базисом (М-метод). | | | Основная теорема теории транспортных задач. Сведение распределительных задач к закрытым транспортным задачам. |