
Читайте также:
|
Для его решения ЗЛП должна содержать единичную подматрицу размером m(на)m – в этом случае очевиден начальный опорный план.
Проверка оптимальности опорного плана происходит с помощью оптимальности. Переход к другому опорному плану проводится с помощью преобразований Гаусса. Полученный опорный план снова проверяется на оптимальность и т.д.
На основании признака оптимальности в базис вводится вектор Ак, давший минимальную отрицательную величину симплекс разности.
Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор Аr, который даёт минимальное положительное оценочное отношение.
Строка Аr называется направляющей, столбец Ак и элемент аrк-направляющим.
Элементы направляющей строки в новой симплекс-таблице вычисляется по формулам:
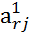 =
= 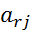 /
/ 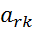
а элементы i-ой строки, по формуле: 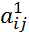 =(
=(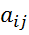 *
* 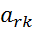 -
- 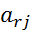 *
* 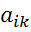 )/
)/ 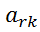
Значения нового опорного плана рассчитываются по формулам:
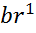 =
=  /
/ 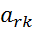
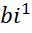 =(
=(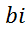 *
* 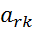 -
- 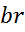 *
* 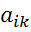 ) /
) / 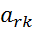
Процесс решения продолжают либо до получения оптимального плана, либо до установления неограниченности целевой функции.
Если среди симплекс-разностей оптимального плана нулевые только оценки, соответствующие базисным векторам, то это значит что оптимальный план единственен. Если же нулевая оценка соответствует вектору, не входящему, то это означает, что оптимальный план не единственный.
Дата добавления: 2015-08-20; просмотров: 61 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Особые случаи при решении задачи ЛП. | | | Симплекс-метод решения задачи с искусственным базисом (М-метод). |