
|
Читайте также: |
Структура является статистической моделью системы и характеризует только строение системы не учитывая множества свойств её элементов.
Математической моделью структуры является граф.
Граф называется конечным, если конечными являются множества его величин и дуг.
Граф называется ориентированным, если 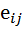 имеет направление, если ориентация не указана, то дуга называется ребром.
имеет направление, если ориентация не указана, то дуга называется ребром.
Ориентированный граф называется- орграфом.
Дуга называется петлёй, если она начинается и заканчивается в одной вершине.
Матрица инциденции орграфа - прямоугольная матрица размером m*n строки которой соответствуют вершинам, а столбцы дугам графа.
Если дуга выходит из вершины, то 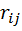 =-1
=-1
Если дуга заходит в вершину, то 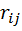 =1
=1
В остальных случаях 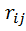 =0
=0
Строки матрицы инциденции называются векторами инциденции.
Матрица смежности вершин орграфа А=[ 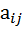 ],
], 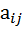 =1, если есть дуга ведущая из
=1, если есть дуга ведущая из 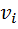 в
в 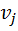 и
и 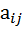 =0
=0
Матрица смежности дуг орграфа B=[ 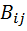 ],
], 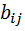 =1, если есть дуга
=1, если есть дуга 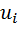 , которая предшествует дуге
, которая предшествует дуге 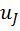 и
и 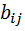 =0
=0
Степень вершины Р- это количество инцидентных ей ребер. Вершина степени 1 называется висячей. Вершина степени 0 называется изолированной.
Дата добавления: 2015-08-20; просмотров: 154 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Описание системы в виде множества элементов | | | Входные и выходные процессы |