Читайте также:
|
Множеством называется совокупность элементов обладающих тремя свойствами:
1.В множестве нет одинаковых элементов
2.Порядок исследования элементов в множестве не имеет значения
3.Любой элемент либо принадлежит, либо не принадлежит рассматривающему множеству
А= [a1,a2,…,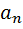 
]
В случае невыполнения 1-го свойства совокупность называется мультимножеством или комплектом.
B={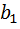 
(
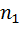)…..bk (nk)}
В случае невыполнения условия 2-го совокупность называется кортежем или вектором.
С=(с1,с2,….,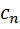 
)
При невыполнении 3-го условия совокупность называется нечетким множеством.
Для построения описания системы в виде множества элементов используют 3 способа:
1.Перечислением элементов
2.Указанием общих свойств элементов
3.Заданием порождающего алгоритма
Единственное, что можно сказать об элементе множества-это входит он или нет в состав других множеств.
Дата добавления: 2015-08-20; просмотров: 78 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Классификация систем | | | Структура как статистическая модель системы. Граф как математическая модель структуры. |