
Читайте также:
|
Вариант 1 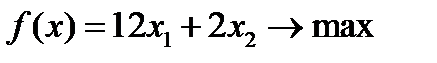 , ,
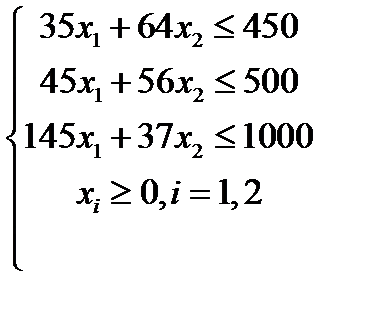
| Вариант 2 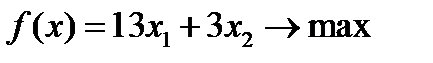 , ,
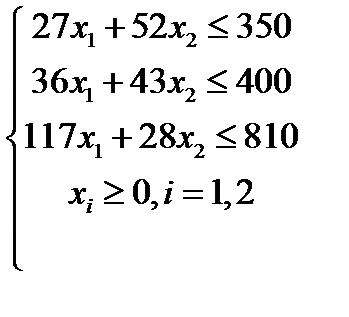
|
Вариант 3 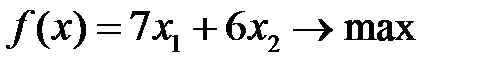 , ,
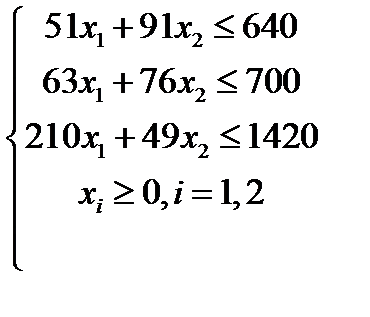
| Вариант 4 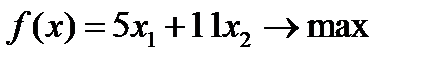 , ,
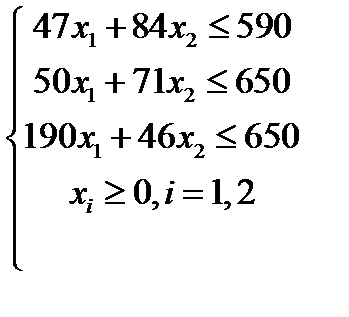
|
Вариант 5 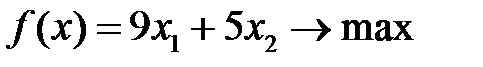 , ,
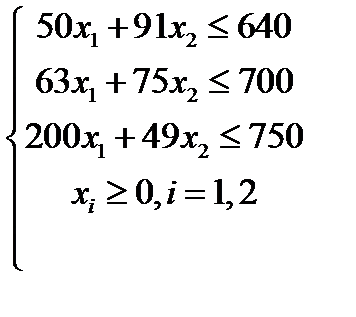
| Вариант 6 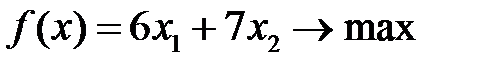 , ,
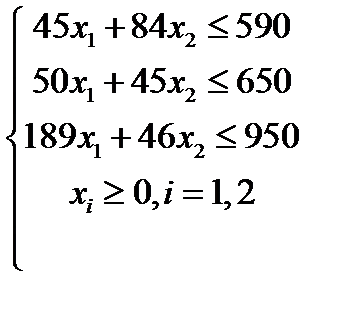
|
Вариант 7 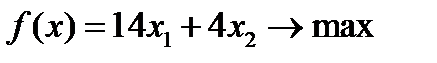 , ,
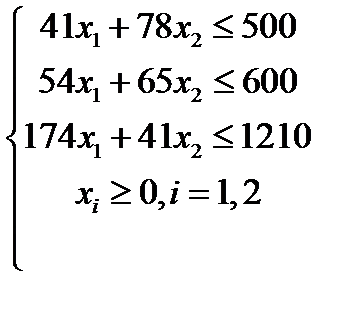
| Вариант 8 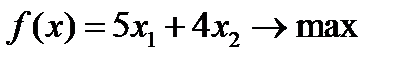 , ,
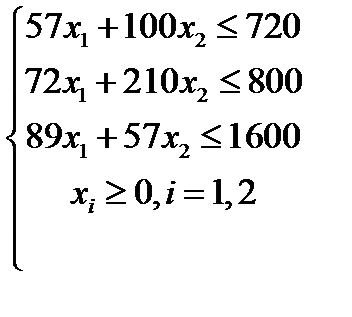
|
Вариант 9 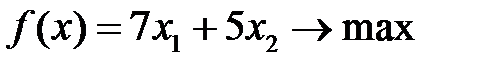 , ,
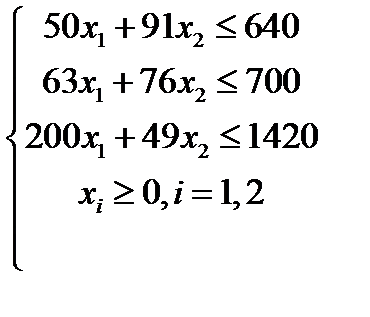
| Вариант 10 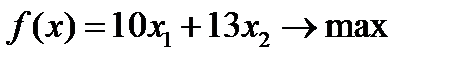 , ,
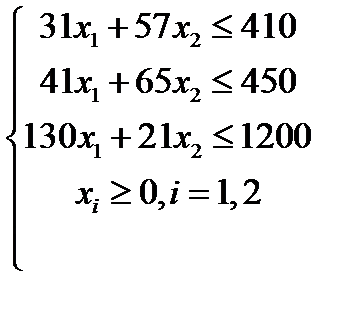
|
Вариант 11 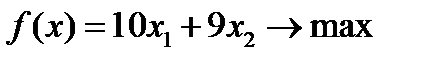 , ,
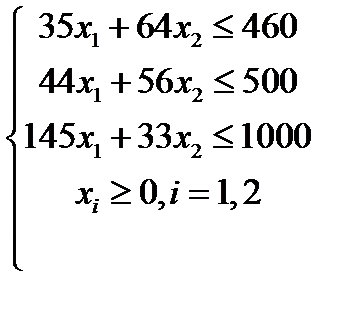
| Вариант 12 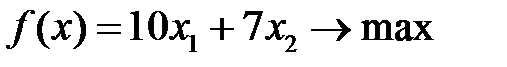 , ,
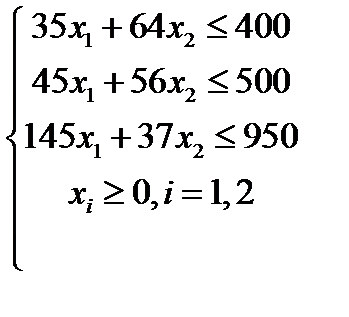
|
Ответы: 1) 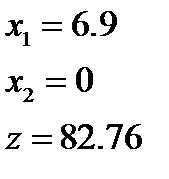 2)
2) 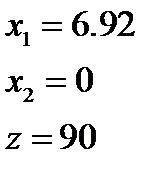 3)
3) 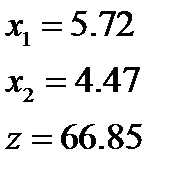 4)
4) 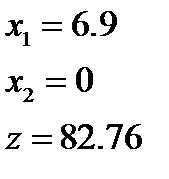 5)
5) 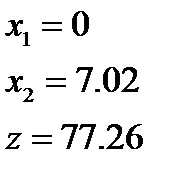 6)
6) 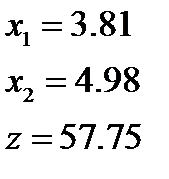
7) 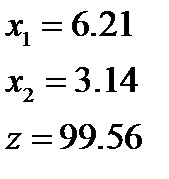 8)
8) 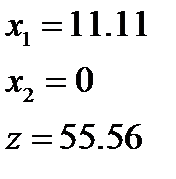 9)
9)  10)
10) 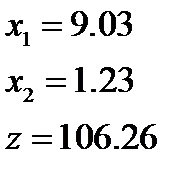 11)
11) 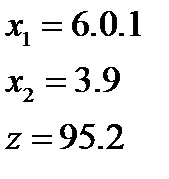
3. Построить и решить задачи, двойственные к данным:
1. Z = х1 - х2 => max 2. Z = 7х1 + 6х2 + 3х3 - х4 => min
х1 - х2 < 1 2х1 - х2 + 2х3 - 3х4 ≥ 12
х1 - х2 ≥ 0 -х1 + 2х2 - х3 + х4 < 10
2х1 < 4 3х1 + 5х2 + 4х4 = 7
х1 ≥ 0, х2 ≥ 0. х1 ≥ 0, х2 ≥ 0, х3 ≥ 0, х4 ≥ 0.
3. Z = х1 - 2х2 + 3х3 - х4 => max 4. Z = 2х1 + 3х2 - х3 + 5х4 => min
2х1 - х2 + 2х3 - 3х4 < 5 5х1 + 4 х2 - 3х3 - х4 = 5
х1 + 2х2 - х3 + х4 < 3 х1 + 2 х2 - х3 < 1
xj ≥ 0 (j = 1, 4) х1 ≥ 0, х2 ≥ 0.
5. Z = 8х1 - 9х2 => max 6. Z = х1 - х2 => min
3х1 + 4х2 < 5 х1 - 4х2 < 5
-х1 + х2 < 7 х1 + 3х2 = 10
6х1 + 2х2 = 1 -3х1 + х2 < 2
х1 ≥ 0, х2 ≥ 0. х1 ≥ 0.
7. Z = -3х1 + 5х2 + х3 + х4 => max 8. Z = 2х1 + 4х2 + х3 => min
3х1 + 8х2 + х3 + х4 < 50 х1 - 2х2 + х3 < 8
5х1 - 4х2 - х3 + х4 ≥ 14 2х1 + 3 х2 - х3 ≥ 1
xj ≥ 0 (j = 1, 4). х1 ≥ 0, х2 ≥ 0.
9. Z = 2х1 + 3х2 => max 10 Z = 9х1 + 12х2 + 10х3 => min
0,5 х1 + х2 < 3 х1 + 3х2 + 4х3 ≥ 60
х1 - 0,5х2 < 4 2х1 + 4х2 + 2х3 ≥ 50
-х1 + х2 < 1,5 х1 + 4х2 + 3х3 ≥ 12
х2 < 2
х2 ≥ 0. xj ≥ 0 (j = 1, 3).
4. Решить задачи дробно-линейного программирования двумя способами:
1. с дробной целевой функцией,
2. предварительно привести к задаче линейного программирования.
. 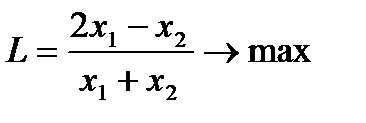
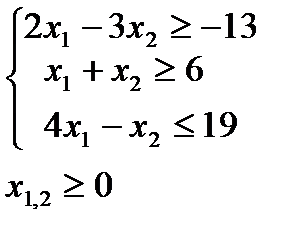 . .
| . 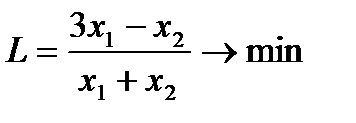
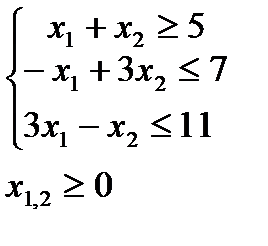 . .
|

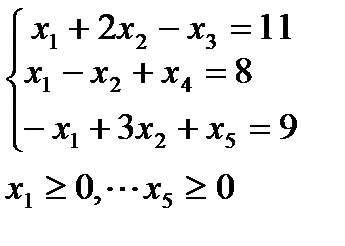
| 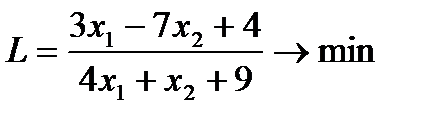
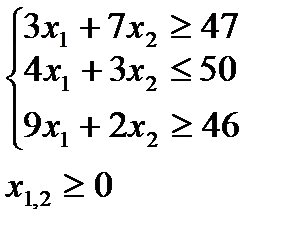 . .
|
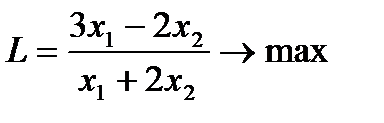
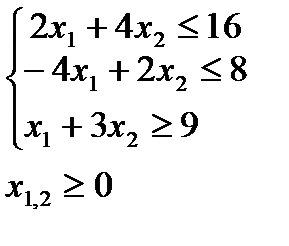
| 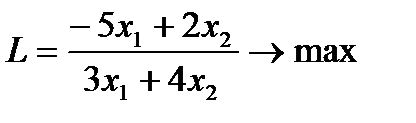
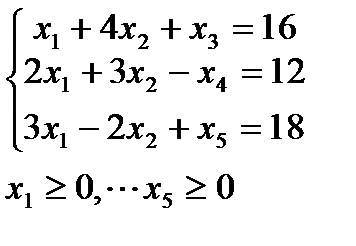
|
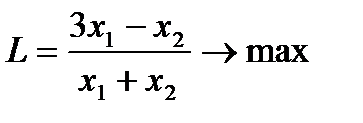
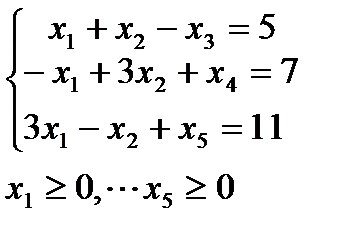
| 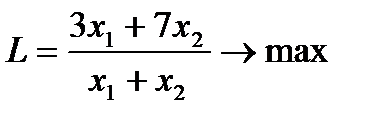

|
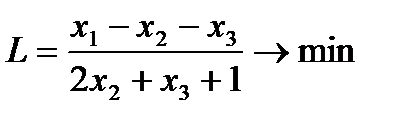
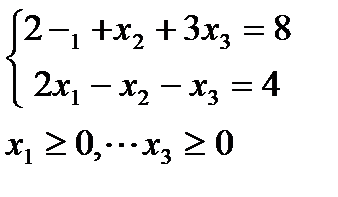
| 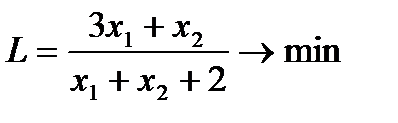
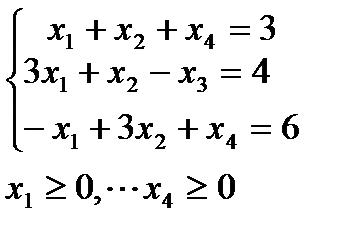
|
Цена 1 м тканей первого типа 2 у. е., второго типа – 2 у. е. В 1 м ткани первого типа содержится 2 ед. натуральных и 2 ед. искусственных волокон. В 1 м ткани второго типа содержится 2 ед. натуральных и 2ед. искусственных волокон. На производство тканей должно быть израсходовано не менее n тыс.ед. натуральных и не более m тыс.ед. искусственных волокон. Определить план производства тканей с общей минимальной себестоимостью.
| n | ||||||||||
| m |
Размещено на Allbest.ru
Дата добавления: 2015-08-20; просмотров: 91 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задания для самостоятельной работы | | | Тестовые задания |