
Читайте также:
|
Неопределённый интеграл.
 Определение. Функция F(x) называется первообразной для функции f(x) на интервале X=(a,b) (конечном или бесконечном), если в каждой точке этого интервала f(x) является производной дляF(x), т.е.
Определение. Функция F(x) называется первообразной для функции f(x) на интервале X=(a,b) (конечном или бесконечном), если в каждой точке этого интервала f(x) является производной дляF(x), т.е.  .
.
 Из этого определения следует, что задача нахождения первообразной обратна задаче дифференцирования: по заданной функции f(x) требуется найти функцию F(x), производная которой равна f(x).
Из этого определения следует, что задача нахождения первообразной обратна задаче дифференцирования: по заданной функции f(x) требуется найти функцию F(x), производная которой равна f(x).
 Первообразная определена неоднозначно: для функции
Первообразная определена неоднозначно: для функции  первообразными будут и функция arctg x, и функция arctg x-10:
первообразными будут и функция arctg x, и функция arctg x-10: 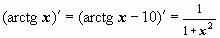 . Для того, чтобы описать все множество первообразных функции f(x), рассмотрим
. Для того, чтобы описать все множество первообразных функции f(x), рассмотрим
 Свойства первообразной.
Свойства первообразной.
1. Если функция F(x) - первообразная для функции f(x) на интервале X, то функция f(x) + C, где C - произвольная постоянная, тоже будет первообразной для f(x) на этом интервале. (Док-во:  ).
).
2. Если функция F(x) - некоторая первообразная для функции f(x) на интервале X=(a,b), то любая другая первообразная F1(x) может быть представлена в виде F1(x) = F(x) + C, где C - постоянная на X функция.
 Из этих свойств следует, что если F(x) - некоторая первообразная функции f(x) на интервале X, то всё множество первообразных функции f(x) (т.е. функций, имеющих производную f(x) и дифференциал f(x) dx) на этом интервале описывается выражением F(x) + C, где C - произвольная постоянная.
Из этих свойств следует, что если F(x) - некоторая первообразная функции f(x) на интервале X, то всё множество первообразных функции f(x) (т.е. функций, имеющих производную f(x) и дифференциал f(x) dx) на этом интервале описывается выражением F(x) + C, где C - произвольная постоянная.
Неопределённый интеграл и его свойства.
 Определение. Множество первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается символом
Определение. Множество первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается символом  .
.
 Как следует из изложенного выше, если F(x) - некоторая первообразная функции f(x), то
Как следует из изложенного выше, если F(x) - некоторая первообразная функции f(x), то  , где C - произвольная постоянная. Функцию f(x) принято называть подынтегральной функцией, произведение f(x) dx - подынтегральным выражением.
, где C - произвольная постоянная. Функцию f(x) принято называть подынтегральной функцией, произведение f(x) dx - подынтегральным выражением.
 Свойства неопределённого интеграла, непосредственно следующие из определения:
Свойства неопределённого интеграла, непосредственно следующие из определения:
1.  .
.
2.  (или
(или  ).
).
Таблица неопределённых интегралов.
 . .
|  . .
| ||
 . .
|  . .
| ||
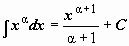 ( ( ). ).
|  . .
| ||
 . .
|  . .
| ||
 ; ; 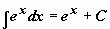 . .
|  . .
| ||
 . .
| 
| ||
 . .
|  . .
| ||
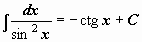 . .
|  . .
| ||
 . .
|  . .
| ||
 . .
|  ; ;  . .
|
В формулах 14, 15, 16, 19 предполагается, что a>0. Каждая из формул таблицы справедлива на любом интервале, на котором непрерывна подынтегральная функция. Все эти формулы можно доказать дифференцированием правой части. Докажем, например, формулу 4: если x > 0, то  ; если x < 0, то
; если x < 0, то  .
.
Простейшие правила интегрирования.
1. 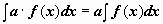 (
( )
)
2. 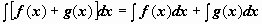
Определённый интеграл
Определение определённого интеграла. Пусть на отрезке [a,b] задана функция y = f(x). Разобьём отрезок [a,b] произвольным образом на n частей точками [x0, x1], [x1, x2], …, [xi-1,xi], …, [xn-1, xn]; длину i-го отрезка обозначим 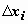 :
:  ; максимальную из длин отрезков обозначим
; максимальную из длин отрезков обозначим  . На каждом из отрезков [xi-1, xi] выберем произвольную точку
. На каждом из отрезков [xi-1, xi] выберем произвольную точку  и составим сумму
и составим сумму 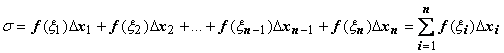 .
.
Сумма  называется интегральной суммой. Если существует (конечный) предел последовательности интегральных сумм
называется интегральной суммой. Если существует (конечный) предел последовательности интегральных сумм  при
при  , не зависящий ни от способа разбиения отрезка [a,b]на части [xi-1, xi], ни от выбора точек
, не зависящий ни от способа разбиения отрезка [a,b]на части [xi-1, xi], ни от выбора точек  , то функция f(x) называется интегрируемой по отрезку [a,b], а этот предел называется определённым интегралом от функции f(x) по отрезку [a,b] и обозначается
, то функция f(x) называется интегрируемой по отрезку [a,b], а этот предел называется определённым интегралом от функции f(x) по отрезку [a,b] и обозначается  .
.
Функция f(x), как и в случае неопределённого интеграла, называется подынтегральной, числа a и b - соответственно, нижним и верхним пределами интегрирования.
Кратко определение иногда записывают так: 
 .
.
В этом определении предполагается, что b> a. Для других случаев примем, тоже по определению:
Если b=a, то  ; еслиb<a, то
; еслиb<a, то  .
.
Свойства определённого интеграла.
1. Линейность. Если функции f(x), g(x) интегрируемы по отрезку [a,b], то по этому отрезку интегрируема их линейная комбинация A f(x) + B g(x) (A, B = const), и

 .
.
2. Аддитивность. Если y = f(x) интегрируема по отрезку [a,b] и точка c принадлежит этому отрезку, то 
 .
.
При формулировании следующих свойств предполагаем, что b > a.
 3. Интеграл от единичной функции (f(x) = 1). Если f(x) = 1, то
3. Интеграл от единичной функции (f(x) = 1). Если f(x) = 1, то  .
.
Вычисление определённого интеграла.
Формула Ньютона-Лейбница. Если f(x) непрерывна на отрезке [a, b], и F(x) - некоторая первообразная функции  , то
, то  .
.
Пример применения формулы Ньютона-Лейбница:
 .
.
Формула интегрирования по частям для определённого интеграла. Если u(x), v(x) - непрерывно дифференцируемые функции, то 
Пример:  .
.
Дата добавления: 2015-08-20; просмотров: 100 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Производные высших порядков. Формула Тейлора | | | Геометрический смысл определенного интеграла. |