Читайте также:
|
Если функция 
имеет производную в каждой точке 
своей области определения, то ее производная 
есть функция от . Функция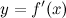 
, в свою очередь, может иметь производную, которую называют производной второго порядка функции (или второй производной) и обозначают символом 
. Таким образом
Пример
Задание. Найти вторую производную функции 
Решение. Для начала найдем первую производную:
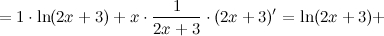
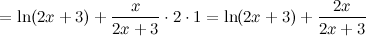
Для нахождения второй производной продифференцируем выражение для первой производной еще раз:
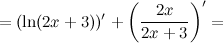
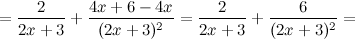
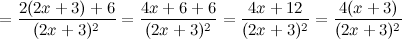
Ответ.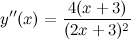 
Больше примеров решенийРешение производных онлайн
Производные более высоких порядков определяются аналогично. То есть производная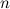 
-го порядка функции 
есть первая производная от производной 
-го порядка этой функции:
Дата добавления: 2015-08-20; просмотров: 75 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задачи на нахождения экстремума функции | | | Неопределенный и определенный интегралы |