Читайте также:
|
Пусть функция y=f(x) имеет производные до n -ого порядка в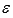 
-окрестности точки 
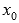и производные до n+1 -ого порядка в самой точке 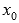. Пусть 
и 
.
Тогда,
· если n – четное, то 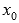- точка перегиба;
· если n – нечетное, то 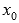- точка экстремума, причем
o если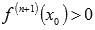 
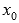, то - точка минимума;
o если 
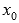, то - точка максимума.
Пример.
Найти точки экстремума функции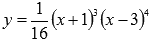 
.
Решение.
Исходная функция является целой рациональной, ее областью определения является все множество действительных чисел.
Продифференцируем функцию:
Производная обращается в ноль при 
, следовательно, это точки возможного экстремума. Воспользуемся третьим достаточным условием экстремума.
Находим вторую производную и вычисляем ее значение в точках возможного экстремума (промежуточные вычисления опустим):
Следовательно, 
- точка максимума (для третьего достаточного признака экстремума имеем n=1 и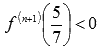 
).
Для выяснения характера точек 
находим третью производную и вычисляем ее значение в этих точках:
Следовательно, 
- точка перегиба функции (n=2 и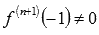 
).
Осталось разобраться с точкой 
. Находим четвертую производную и вычисляем ее значение в этой точке:
Следовательно, - точка минимума функции.
Дата добавления: 2015-08-20; просмотров: 98 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Второй признак экстремума функции. | | | Точки экстремума |