Второй признак экстремума функции.

Пусть ,

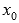· если , то - точка минимума;

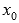· если , то - точка максимума.

Как видите, этот признак экстремума функции требует существования производной как минимум до второго порядка в точке .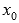

Пример.

Найти экстремумы функции .

Решение.

Начнем с области определения:

Продифференцируем исходную функцию:

Производная обращается в ноль при x=1, то есть, это точка возможного экстремума. Находим вторую производную функции и вычисляем ее значение при x = 1:

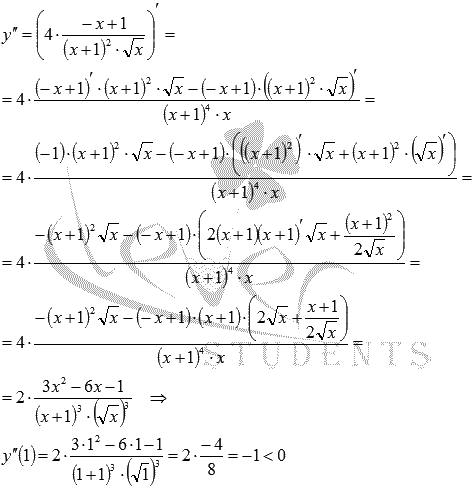
Следовательно, по второму достаточному условию экстремума, x=1 - точка максимума. Тогда - максимум функции.

Дата добавления: 2015-08-20