Непрерывность элементарных функций

Важнейшим свойством всех элементарных функций является их непрерывность в каждой точке определения. Убедимся в этом на примере некоторых элементарных функций .Рациональные функции . 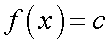— непрерывна во всех точках, поскольку для любого значения аргумента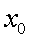 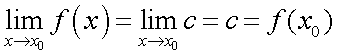. 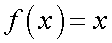— непрерывна во всех точках, так как 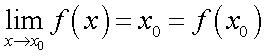. 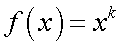— непрерывна по теореме о произведении непрерывных функций.Многочлен 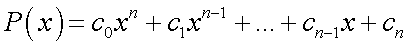— непрерывен по теореме о сумме (разности) непрерывных функций.По теореме о частном непрерывных функций дробно-рациональная функция 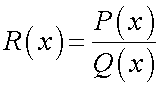— непрерывна везде, где 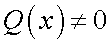.Тригонометрические функции . 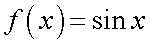, 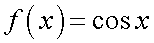— непрерывны всюду. Рассмотрим функцию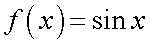 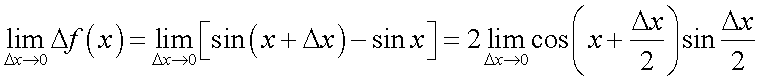.Так как 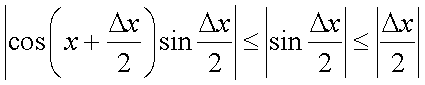, а последнее выражение стремится к нулю при 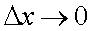, то и 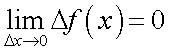. Неравенство 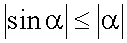следует из того что синус угла α (отсчитываемый от направления оси абсцисс) представляет собой величину ординаты точки на единичной окружности, а угол α есть длина дуги этой окружности.Аналогично доказывается непрерывность 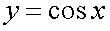.По теореме о частном непрерывных функций тригонометрические функции 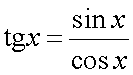, 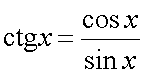— непрерывны всюду, где знаменатель не обращается в ноль. 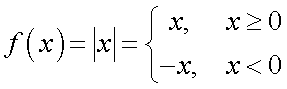— непрерывна всюду, так как 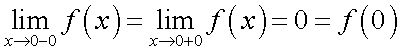, а непрерывность при 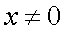очевидна. Вычисление пределов непрерывных функций Для непрерывных функций задача вычисления предела становится тривиальной. Если известно, что функция 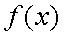непрерывна в некоторой точке 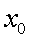, то ее предел 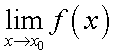в этой точке может быть вычислен нахождением значения функции в этой точке 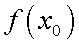. Пример 1.Найти предел 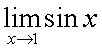. Поскольку 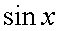является непрерывной функцией, можем сразу найти предел 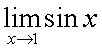= 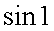. Пример 2.Найти предел 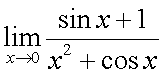. И в числителе, и в знаменателе стоят непрерывные функции. Поскольку знаменатель отличен от нуля в точке 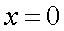, можем воспользоваться теоремой о пределе частного и записать 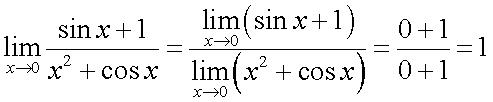. Пример 3.Найти предел 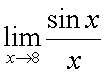. И в числителе, и в знаменателе стоят непрерывные функции. Поскольку знаменатель отличен от нуля в точке 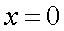, можем воспользоваться теоремой о пределе частного и записать = .

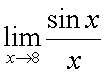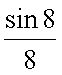Дата добавления: 2015-08-20