Читайте также:
|
Найти общий член последовательности 
Р е ш е н и е: не трудно видеть, что
, 
, 
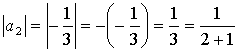
и т.д.
Следовательно:
Пример 3.
Доказать, что последовательность с общим членом 
имеет предел, равный нулю.
Р е ш е н и е: запишем ряд членов последовательности
и положим 
. Для всех членов данной последовательности, начиная с четвертого, выполняется равенство
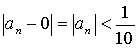
Действительно
и т.д.
В данном случае N (см. определение предела последовательности) можно принять равным трем (или любому числу, больше трех), так как, если порядковый номер члена последовательности n больше трех, то выполняется неравенство
.
Положим теперь 
. Ясно, что для всех членов последовательности начиная с седьмого,
.
Теперь за N можно принять шесть (или любое число, большее шести). Если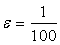 
, то 
и т.д.
В данном случае можно найти общее выражение для числа N в зависимости от 
. Общий член данной последовательности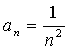 
. Задавшись произвольным положительным числом 
, мы должны в соответствии с определением предела, потребовать, чтобы при n > N выполнялось неравенство 
, если 
.
Решая неравенство относительно n, получаем 
. Итак, за N можно принять число 
(или любое большее число). Таким образом, мы показали, что для любого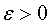 
существует такое 
, чтопри 
, выполняется неравенство 
, а это и доказывает, что пределом последовательности является нуль.
Отметим, что в этой задаче члены последовательности приближались к своему пределу, оставаясь больше этого предела, как говорят, справа.
Дата добавления: 2015-08-20; просмотров: 52 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Числовая последовательности и ее предел. | | | Табличный способ |