|
Читайте также: |
Ответ:
.
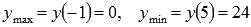ОБРАТИТЕ ВНИМАНИЕ: первый достаточный признак экстремума не требует дифференцируемости функции в самой точке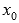 
.
Пример.
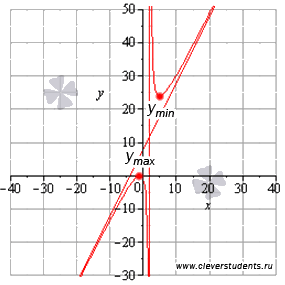
Найдите точки экстремума и экстремумы функции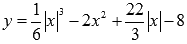 
.
Решение.
Областью определения функции является все множество действительных чисел. Саму функцию можно записать в виде:
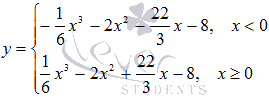
Найдем производную функции:
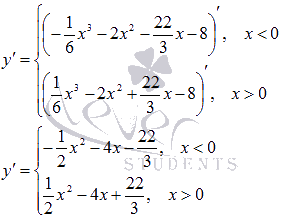
В точке x=0 производная не существует, так как значения односторонних пределов при стремлении аргумента к нулю не совпадают:
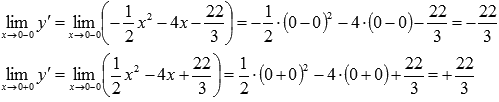
В это же время, исходная функция является непрерывной в точке x=0 (смотрите разделисследование функции на непрерывность):
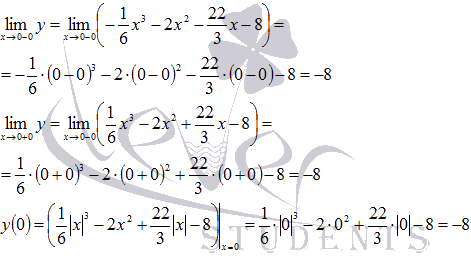
Найдем значения аргумента, при котором производная обращается в ноль:
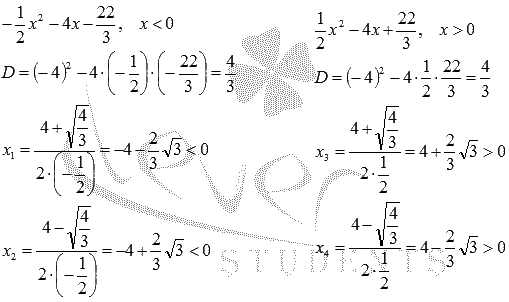
Отметим все полученные точки на числовой прямой и определим знак производной на каждом из интервалов. Для этого вычислим значения производной в произвольных точках каждого интервала, к примеру, при x=-6, x=-4, x=-1, x=1, x=4, x=6.
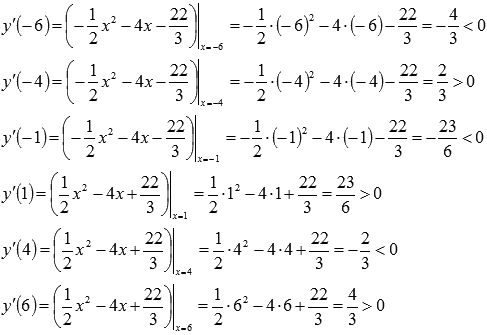
То есть,
Таким образом, по первому признаку экстремума, точками минимума являются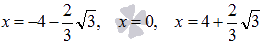 
, точками максимума являются 
.
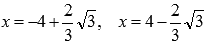Вычисляем соответствующие минимумы функции
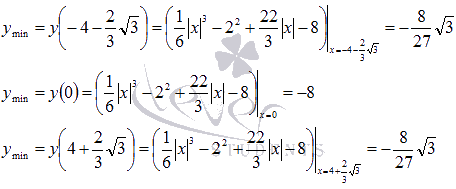
Вычисляем соответствующие максимумы функции
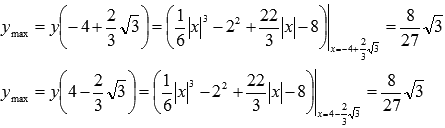
Дата добавления: 2015-08-20; просмотров: 64 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Алгоритм нахождения точек экстремума по первому признаку экстремума функции. | | | Второй признак экстремума функции. |