
Читайте также:
|
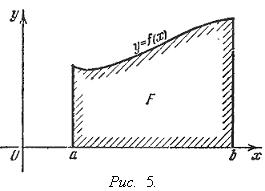
Если f (x) непрерывна и положительна на [ a, b ], то интеграл


представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f (x) (см. рис. 5.).
Не следует думать, что условие непрерывности функции необходимо для того, чтобы у нее существовал определенный интеграл. Интеграл может существовать и у разрывной функции. Пусть, например, функция f (x), заданная на промежутке [ a, b ], равна нулю во всех точках этого промежутка, кроме конечного числа точек z 1, z 2,..., zN. Составим для f (x) интегральную сумму σ.
Пусть из точек ξ 0, ξ 1,..., ξn -1, входящих в определение σ, p точек совпадают с точками zi, а остальные отличны от них. Тогда в сумме σ будет лишь p слагаемых, отличных от нуля. Если наибольшее из чисел | f (zi) | (i = 1, 2,..., N) есть K, то, очевидно,
| σ | ≤ Kpλ ≤ KNλ,
откуда ясно, что при λ → 0 будет и σ → 0. Таким образом, интеграл


существует и равен нулю.
Приведем теперь пример функции, не имеющей интеграла. Пусть φ (x) задана на промежутке [0, 1] так:



Если мы, составляя сумму σ, за точки ξk выберем числа иррациональные, то окажется σ = 0. Если же все ξk взять рациональными, то получится σ = 1. Таким образом, за счет одного лишь уменьшения λ нельзя приблизить σ к какому-либо постоянному числу, и интеграл


не существует.
В настоящее время известны точные признаки, позволяющие судить, имеет или нет заданная функция определенный интеграл, но мы ограничимся вышеприведенной теоремой об интегрируемости непрерывных функций.
14.Определение числового ряда.
Сходимость ряда.
Бесконечным числовым рядом называется выражение
| u1+u2+...+un+..., | (1) |
содержащее неограниченное число членов, где
u1, u2, u3,..., un,...
- бесконечная числовая последовательность; un называется общим членом ряда.
Для составления ряда нужно знать закон образования общего члена.
Например, если un = 2*n+1, то ряд имеет вид:
3, 5, 7, 9,..., 501, 503,..., n*2+1
Если un = (-1)n, то ряд имеет вид:
-1, +1, -1, +1,..., -1, +1,..., (-1)n
Сумма первых n членов ряда обозначается символом Sn и называется частичной суммой этого ряда. Таким образом,
Sn = u1 + u2 +... + u n
или, короче,
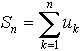
Определение: Ряд называется сходящимся, если сумма первых его n членов при n ®¥ стремится к конечному пределу S, называемому суммой ряда.
Если ряд (1) сходится, т.е. имеет сумму S, то пишут
S = u1 + u2 +... + u n +...
Если же при n ®¥ сумма Sn не имеет предела или

то ряд (1) называется расходящимся и не имеет суммы.
Типичным примером сходящегося ряда может служить ряд, полученный из бесконечно убывающей геометрической прогрессии
| a + aq + aq 2 + aq 3 +... + aq n-1 +..., | (2) |
где
-1 < q < 1
Действительно, для этого ряда
|
При n ®¥ qn ® 0 (так как | q |<1), поэтому

и ряд (2) будет сходящимся. Таким образом можно написать
|
Если q = 1, то ряд (2) имеет вид
| a + a + a + a +... + a +.... | (3) |
Сумма Sn первых его n членов, равная na, по абсолютной величине неограниченно возрастает при неограниченном возрастании числа n. Таким образом, ряд (3) - расходящийся.
Если q = -1, то ряд (2) примет вид
| a - a + a - a + a - a +... +(-1)n-1 a +.... | (4) |
Ясно, что для этого ряда
S2n=0, S2n-1=a.
т.е.сумма четного числа первых 2n членов ряда (4) стремится к нулю, а сумма нечетного числа первых 2n-1 его членов стремится к a.
Отсюда следует, что ряд (4) расходится, так как в сходящемся ряде как S2n так и S2n-1 стремятся к одному и тому же пределу S.
Ясно, что если | q |>1, то ряд (2) является также расходящимся.
Дата добавления: 2015-08-20; просмотров: 50 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Неопределенный и определенный интегралы | | | Признак сходимости Даламбера и Коши |