
Читайте также:
|
Функция
 (2.3.1)
(2.3.1)
называется функцией Жуковского.
Эта функция была введена в рассмотрение русским ученым Н.Е. Жуковским в теории крыла самолета и имела важные приложения, поэтому носит его имя.Эта функция регулярна в точках 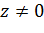 , ∞, причем
, ∞, причем  в точках
в точках 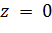 и
и  имеет полюсы первого порядка. Следовательно, функция Жуковского (1) однолистна в каждой точке
имеет полюсы первого порядка. Следовательно, функция Жуковского (1) однолистна в каждой точке  , так как
, так как  при
при  , и неоднолистна в точках
, и неоднолистна в точках  ,, так как
,, так как 
Рассмотрим основные свойства функции Жуковского.
1. Однолистность.
Функция Жуковского  однолистна в области
однолистна в области  тогда и только тогда, когда в этой области нет различных точек
тогда и только тогда, когда в этой области нет различных точек  и
и  , связанных равенством
, связанных равенством
 (2.3.2)
(2.3.2)
В самом деле, пусть  . Тогда
. Тогда  , откуда либо
, откуда либо  , либо
, либо  .
.
 |
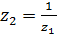 , получается из точки
, получается из точки  двойной симметрией: относительно окружности
двойной симметрией: относительно окружности  и относительно прямой
и относительно прямой  (Рис. 2.3.1).
(Рис. 2.3.1).
Рисунок 2.3.1.
Таким образом, функция Жуковского однолистна в области в том и только в том случае, когда эта область не содержит ни одной пары различных точек, которые получаются одна из другой двойной симметрией: относительно единичной окружности и относительно действительной оси.
Функция Жуковского  однолистна в следующих областях:
однолистна в следующих областях:
·  — внешность единичного круга,
— внешность единичного круга,
·  — внутренность единичного круга,
— внутренность единичного круга,
·  — верхняя полуплоскость
— верхняя полуплоскость
·  — нижняя полуплоскость
— нижняя полуплоскость
2. Образы окружностей и лучей.
Найдем образы окружностей  и лучей
и лучей  (полярная координатная сетка) при отображении функцией Жуковского. Полагая в (3.3.1)
(полярная координатная сетка) при отображении функцией Жуковского. Полагая в (3.3.1) 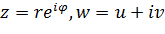 , получаемы
, получаемы  , откуда применив формулы Эйлера получим:
, откуда применив формулы Эйлера получим:
 ,
,  (2.3.3)
(2.3.3)
Рассмотрим окружность
 (2.3.4)
(2.3.4)
( — фиксировано). Из (3.3.3) следует, что при отображении функцией Жуковского образом окружности (3.3.4) является эллипс
— фиксировано). Из (3.3.3) следует, что при отображении функцией Жуковского образом окружности (3.3.4) является эллипс
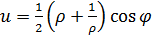 ,
,  (2.3.5)
(2.3.5)
с полуосями 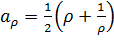 ,
,  и с фокусами в точках
и с фокусами в точках  (так как
(так как 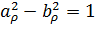 ). Исключаяиз уравнений (3.3.5) параметр
). Исключаяиз уравнений (3.3.5) параметр  , при
, при  уравнение этого эллипса можно записать в каноническом виде:
уравнение этого эллипса можно записать в каноническом виде:
 (2.3.6)
(2.3.6)
Отметим, что при замене 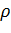 на
на  эллипс (2.3.5) остается тем же самым, но его ориентация меняется на противоположную. На рис. 2.3.2 показаны окружности
эллипс (2.3.5) остается тем же самым, но его ориентация меняется на противоположную. На рис. 2.3.2 показаны окружности  , ориентированные по часовой стрелке, и их образы — эллипсы (2.3.6)
, ориентированные по часовой стрелке, и их образы — эллипсы (2.3.6)

Рисунок 2.3.2.

Из (2.3.5) видно, что эти эллипсы ориентированы также по часовой стрелке. На рис. 2.3.3 показаны окружности  при
при  и их образы — эллипсы (2.3.6); при этом ориентация меняется на противоположную: окружность
и их образы — эллипсы (2.3.6); при этом ориентация меняется на противоположную: окружность  , ориентированная против часовой стрелки, переходит в эллипс (2.3.6), ориентированный по часовой стрелке.
, ориентированная против часовой стрелки, переходит в эллипс (2.3.6), ориентированный по часовой стрелке.
Рисунок 2.3.3.
При  эллипс (3.3.5) вырождается в отрезок
эллипс (3.3.5) вырождается в отрезок  проходимый дважды, т. е. окружность
проходимый дважды, т. е. окружность  переходит в отрезок [—1, 1], проходимый дважды (рис. 3.3.2, 3.3.3).
переходит в отрезок [—1, 1], проходимый дважды (рис. 3.3.2, 3.3.3).
Рассмотрим луч
 (2.3.7)
(2.3.7)
(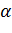 — фиксировано). При отображении функцией Жуковского образом этого луча (см. (3.3.3)) является кривая
— фиксировано). При отображении функцией Жуковского образом этого луча (см. (3.3.3)) является кривая
 ,
,  (2.3.8)
(2.3.8)
Исключаяиз уравнений (3.3.8) параметр  , при
, при 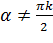 (
( — целое), получаем
— целое), получаем
 (2.3.9)
(2.3.9)
Кривая (2.3.9) — гипербола с фокусами в точках  и с асимптотами
и с асимптотами  .
.
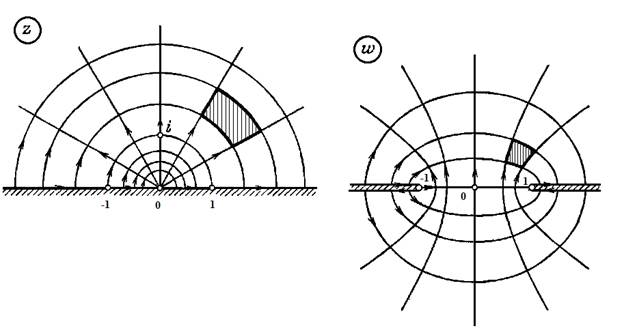
Если  , то кривая (2.3.8) является правой ветвью гиперболы (2.3.9), т. е. луч (2.3.7) при
, то кривая (2.3.8) является правой ветвью гиперболы (2.3.9), т. е. луч (2.3.7) при  переходит в правую ветвь гиперболы (2.3.9) (ориентация показана на рис. 2.3.4).
переходит в правую ветвь гиперболы (2.3.9) (ориентация показана на рис. 2.3.4).
Рисунок 2.3.4.
При замене в (2.3.8) 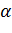 на
на  получается левая ветвь той же гиперболы (2.3.9), поэтому луч (2.3.7) при
получается левая ветвь той же гиперболы (2.3.9), поэтому луч (2.3.7) при  переходит в левую ветвь гиперболы (2.3.9) (рис. 2.3.4). Отметим также, что при замене в (2.3.8)
переходит в левую ветвь гиперболы (2.3.9) (рис. 2.3.4). Отметим также, что при замене в (2.3.8) 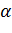 на
на  получается та же ветвь гиперболы (2.3.9), но ее ориентация меняется на противоположную.
получается та же ветвь гиперболы (2.3.9), но ее ориентация меняется на противоположную.
Рассмотрим лучи (2.3.7) при  (
( — целое). Из (2.3.8) следует, что луч
— целое). Из (2.3.8) следует, что луч  переходит в мнимую ось
переходит в мнимую ось  (рис. 2.3.4). Луч
(рис. 2.3.4). Луч  также переходит в мнимую ось
также переходит в мнимую ось  . При
. При  кривая (2.3.8) вырождается в луч
кривая (2.3.8) вырождается в луч  проходимый дважды (сложенный вдвое) (рис. 2.3.4), т. е. луч
проходимый дважды (сложенный вдвое) (рис. 2.3.4), т. е. луч  переходит в луч
переходит в луч  , проходимый дважды: луч
, проходимый дважды: луч  переходит в луч
переходит в луч  и полуинтервал
и полуинтервал 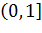 – в луч
– в луч  (рис. 2.3.4). Аналогично, луч
(рис. 2.3.4). Аналогично, луч  переходит в луч
переходит в луч 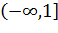 , проходимый дважды (рис. 2.3.4).
, проходимый дважды (рис. 2.3.4).
Таким образом, функция Жуковского  переводит окружности
переводит окружности  в эллипсы (2.3.6), а лучи
в эллипсы (2.3.6), а лучи  – в ветви гипербол (2.3.9); фокусы всех эллипсов (2.3.6) и гипербол (2.3.9) расположены в точках
– в ветви гипербол (2.3.9); фокусы всех эллипсов (2.3.6) и гипербол (2.3.9) расположены в точках  ; любой эллипс (2.3.6) пересекается с любой гиперболой (2.3.9) под прямым углом.
; любой эллипс (2.3.6) пересекается с любой гиперболой (2.3.9) под прямым углом.
4. Функция 
Рассмотрим основные свойства данной функции.
1. Однолистность.
Найдем условие, которому должна удовлетворять область  , чтобы отображение
, чтобы отображение
 (3.1.1)
(3.1.1)
было однолистным в этой области.
Если  , т.е.
, т.е.  , то
, то
 (3.1.2)
(3.1.2)
Следовательно, для однолистности отображения (3.1.1) необходимо и достаточно, чтобы область  не содержала никакой пары различных точек, удовлетворяющих условию (3.1.2).
не содержала никакой пары различных точек, удовлетворяющих условию (3.1.2).
2. Периодичность.
По формуле Эйлера 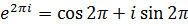 =1, то для любого
=1, то для любого  имеем
имеем  .
.
С другой стороны, пусть  . Умножая обе части на
. Умножая обе части на 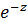 получаем
получаем  откуда, полагая
откуда, полагая  , имеем
, имеем  . Но тогда
. Но тогда 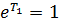 , то есть
, то есть  и
и  =1 и
=1 и  , то есть
, то есть  , где
, где  – целое число. Таким образом,
– целое число. Таким образом,  и
и  являются основными периодами.
являются основными периодами.
3. Конформность.
Так как производная функции (3.1.1) во всех точках отлична от нуля, то отображение конформно во всех точках конечной плоскости  .
.
4. Образы точек конечной плоскости.
Рассмотрим отображения, осуществляемые посредством этой функции. Заметим, что функция никогда не принимает значение  . Это значит, что начало координат плоскости
. Это значит, что начало координат плоскости 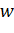 не принадлежит к образу конечной плоскости
не принадлежит к образу конечной плоскости  при отображении (3.1.1). Покажем, что всякая другая конечная точка плоскости
при отображении (3.1.1). Покажем, что всякая другая конечная точка плоскости 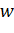 принадлежит к этому образу. В самом деле, из уравнения
принадлежит к этому образу. В самом деле, из уравнения  , где
, где  задано, а
задано, а  – неизвестное, получаем:
– неизвестное, получаем:
 , откуда
, откуда  и
и  , то есть
, то есть  .
.
Итак, прообразами точек 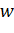 могут быть только точки вида
могут быть только точки вида
 .
.
Очевидно, их бесконечно много, так как 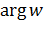 имеет бесконечное множество значений, различающиеся попарно на целые кратные
имеет бесконечное множество значений, различающиеся попарно на целые кратные  . Кроме того, каждая из найденных точек действительно есть прообраз точки
. Кроме того, каждая из найденных точек действительно есть прообраз точки 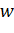 , так как
, так как
 . (3.1.3)
. (3.1.3)
Итак, множество всех корней уравнения  , где
, где  представляются формулой
представляются формулой
 =
= 
Все эти точки расположены на одной прямой, параллельной мнимой оси на расстоянии  друг от друга.
друг от друга.
То есть функция (3.1.1) отображает конечную плоскость  на область, получающуюся из конечной плоскости
на область, получающуюся из конечной плоскости 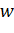 путем исключения одной точки
путем исключения одной точки  , при чем отображение не взаимно однозначно, так как каждая точка
, при чем отображение не взаимно однозначно, так как каждая точка  имеет бесконечное множество прообразов (3.1.3).
имеет бесконечное множество прообразов (3.1.3).
5. Образы прямых, параллельных осям координат.

Заставим  описывать какую-нибудь прямую, параллельную одной из координатных осей (Рис. 3.1.1).
описывать какую-нибудь прямую, параллельную одной из координатных осей (Рис. 3.1.1).
Рисунок 3.1.1.
Если это будет прямая 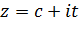 , параллельная мнимой оси, то
, параллельная мнимой оси, то  , то есть
, то есть 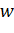 будет находиться на окружности с центром в начале координат и радиусом, равным
будет находиться на окружности с центром в начале координат и радиусом, равным  . При этом, когда точка
. При этом, когда точка  описывает прямую однократно так, что ордината этой точки, равная
описывает прямую однократно так, что ордината этой точки, равная  , непрерывно растет от -∞ до +∞, то
, непрерывно растет от -∞ до +∞, то 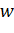 описывает соответствующую окружность бесконечное множество раз в одном и том же положительном направлении.
описывает соответствующую окружность бесконечное множество раз в одном и том же положительном направлении.
Если же точка  описывает прямую
описывает прямую 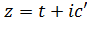 , параллельную действительной оси, то
, параллельную действительной оси, то  , очевидно, пробегает прямолинейный луч, выходящий из начала координат и образующий с положительной частью действительной оси угол
, очевидно, пробегает прямолинейный луч, выходящий из начала координат и образующий с положительной частью действительной оси угол  . При этом, когда точка
. При этом, когда точка  описывает однократно так, что абсцисса этой точки, равная
описывает однократно так, что абсцисса этой точки, равная  , непрерывно растет от -∞ до +∞, то
, непрерывно растет от -∞ до +∞, то 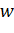 описывает соответствующий луч однократно так, что расстояние этой точки от начала координат непрерывно растет от 0до ∞ (и тот и другой пределы исключаются, так как
описывает соответствующий луч однократно так, что расстояние этой точки от начала координат непрерывно растет от 0до ∞ (и тот и другой пределы исключаются, так как 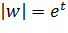 ).
).
Итак, при отображении плоскости  посредством функции
посредством функции  семейство прямых, параллельных мнимой оси преобразуется в семейство окружностей с центром в начале координат, а семейство прямых, параллельных действительной оси, – в семейство прямолинейных лучей, выходящих из начала координат.
семейство прямых, параллельных мнимой оси преобразуется в семейство окружностей с центром в начале координат, а семейство прямых, параллельных действительной оси, – в семейство прямолинейных лучей, выходящих из начала координат.
6. Образы полос, параллельных действительной оси.
 |
 , представляющую внутренность прямоугольной полосы шириной
, представляющую внутренность прямоугольной полосы шириной  , параллельной действительной оси. Пусть эта полоса ограничена линиями
, параллельной действительной оси. Пусть эта полоса ограничена линиями  и
и  . Из установленного выше следует, что образ области
. Из установленного выше следует, что образ области  в плоскости
в плоскости  будет область
будет область  , представляющая угол раствора
, представляющая угол раствора  с вершиной в начале координат, ограниченный прямолинейными лучами
с вершиной в начале координат, ограниченный прямолинейными лучами  и
и  (Рис. 3.1.2).
(Рис. 3.1.2).
Рисунок 3.1.2.
При этом соответствие между точками областей  и
и  , устанавливаемое посредством функции (3.4.1.), будет взаимно однозначным, поскольку прообразами некоторой точки
, устанавливаемое посредством функции (3.4.1.), будет взаимно однозначным, поскольку прообразами некоторой точки  из области
из области  могут быть только точки
могут быть только точки  , различающиеся друг от друга значениями мнимой части. Две такие точки лежат на одной прямой, параллельной мнимой оси, на расстоянии, кратном
, различающиеся друг от друга значениями мнимой части. Две такие точки лежат на одной прямой, параллельной мнимой оси, на расстоянии, кратном  . Но полоса
. Но полоса  имеет ширину не более
имеет ширину не более  , поэтому она может содержать внутри лишь один прообраз точки
, поэтому она может содержать внутри лишь один прообраз точки  . Итак, каждая точка
. Итак, каждая точка  имеет лишь один образ и каждая точка
имеет лишь один образ и каждая точка  лишь один прообраз внутри
лишь один прообраз внутри  , что выражает взаимную однозначность отображения.
, что выражает взаимную однозначность отображения.
При этом показательная функция взаимно однозначно и конформно отображает полосу ширины  , параллельную действительной оси, на угол раствора
, параллельную действительной оси, на угол раствора  с вершиной в начале координат. Поэтому к показательной функции прибегают каждый раз, когда надо отобразить некоторую прямолинейную полосу на внутренность угла.
с вершиной в начале координат. Поэтому к показательной функции прибегают каждый раз, когда надо отобразить некоторую прямолинейную полосу на внутренность угла.
7. Образ прямой, не параллельной ни одной из оси координат.
Если прямая плоскости  не является параллельной какой-либо оси координат, то образ её в плоскости
не является параллельной какой-либо оси координат, то образ её в плоскости  будет уже не прямой и не окружностью, а логарифмической спиралью. В самом деле, если эта прямая есть
будет уже не прямой и не окружностью, а логарифмической спиралью. В самом деле, если эта прямая есть  (
(  – угловой коэффициент прямой, а
– угловой коэффициент прямой, а 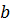 – ордината в начале), то образом будет кривая
– ордината в начале), то образом будет кривая  . Здесь
. Здесь  ,
,  , или, исключая параметр
, или, исключая параметр  :
:  . Но
. Но  или полярный угол
или полярный угол  определен только с точностью до целого кратного от
определен только с точностью до целого кратного от  . Поэтому, обозначая
. Поэтому, обозначая 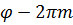 снова через
снова через  получаем:
получаем: 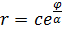 , где
, где 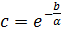 .
.
Это и есть уравнение логарифмической спирали (Рис. 3.1.3). Из того, что она является образом прямой есть  пересекающей прямые, параллельные действительной оси под постоянным углом
пересекающей прямые, параллельные действительной оси под постоянным углом 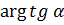 , следует в силу конформности отображения, что и логарифмическая спираль пересекается под тем же углом образы указанных прямых, то есть все лучи, выходящие из начала координат. Мы получили характеристическое свойство логарифмической спирали.
, следует в силу конформности отображения, что и логарифмическая спираль пересекается под тем же углом образы указанных прямых, то есть все лучи, выходящие из начала координат. Мы получили характеристическое свойство логарифмической спирали.
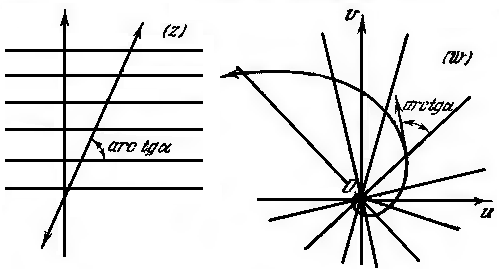
Рисунок 3.1.3.

Пример 3.1.1. Из приведенных свойств (1) и (2) вытекает, что функция  конформно отображает прямоугольник
конформно отображает прямоугольник  ,
,  , где
, где 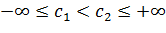 ,
,  на кольцевой сектор
на кольцевой сектор  . Частные случаи таких отображений показаны на рис. 3.1.4.
. Частные случаи таких отображений показаны на рис. 3.1.4.
Рисунок 3.1.4.
Пример 3.1.2. Найдем образ отрезка  при отображении
при отображении  .
.
 |
Любая точка отрезка имеет комплексную координату  ,
,  . Поэтому её образом служит линия, параметрически заданная уравнениями
. Поэтому её образом служит линия, параметрически заданная уравнениями  . Это дуга логарифмической спирали (рис. 3.4.5).
. Это дуга логарифмической спирали (рис. 3.4.5).
5. Тригонометрические функции  и
и 
Тригонометрические функции в комплексной области просто выражаются через показательную функцию. По формуле Эйлера имеем: 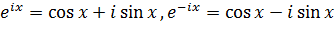 , откуда
, откуда  ,
,  .
.
Учитывая это, примем по определению для любого комплексного 
 ,
,  . (3.2.1)
. (3.2.1)
Отметим, что функции (3.2.1) периодичны с периодом  .
.
Рассмотрим функция  . Эту функцию можно представит в виде суперпозиции функций:
. Эту функцию можно представит в виде суперпозиции функций:
 (3.25.2)
(3.25.2)
В силу периодичности функции  , она не является однолистной на всей комплексной плоскости
, она не является однолистной на всей комплексной плоскости  . Можно разбить комплексную плоскость
. Можно разбить комплексную плоскость  на счетное число областей
на счетное число областей  – вертикальные полосы:
– вертикальные полосы:  (рис.3.2.1).
(рис.3.2.1).

Рисунок 3.2.1.
Функция  каждую область
каждую область  k переводит на всю комплексную плоскость
k переводит на всю комплексную плоскость  с двумя выброшенными лучами:
с двумя выброшенными лучами:  .
.
Если рассмотреть нижнюю полуполосу 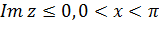 , то функция
, то функция  переводит ее на верхнюю полуплоскость
переводит ее на верхнюю полуплоскость  .
.
Рассмотрим функцию  . Полагая, что
. Полагая, что
 (3.2.3)
(3.2.3)
получим:
 . (3.2.4)
. (3.2.4)
То есть отображение  можно рассматривать как суперпозицию уже рассмотренных отображений.
можно рассматривать как суперпозицию уже рассмотренных отображений.
Найдем условия его однолистности. Пусть область  при отображениях (3.2.3) переходит последовательно в
при отображениях (3.2.3) переходит последовательно в  . Первое и третье из отображений (3.2.3) однолистны всюду. Для однолистности второго необходимо и достаточно, чтобы
. Первое и третье из отображений (3.2.3) однолистны всюду. Для однолистности второго необходимо и достаточно, чтобы  не содержало ни одной пары точек
не содержало ни одной пары точек  , для которых
, для которых  . Переходя с помощью формул (3.2.3) к плоскости
. Переходя с помощью формул (3.2.3) к плоскости  , получим, что для однолистности (3.2.4) в области
, получим, что для однолистности (3.2.4) в области  необходимо и достаточно, чтобы
необходимо и достаточно, чтобы  не содержало ни одной из точек
не содержало ни одной из точек  , для которых, с одной стороны
, для которых, с одной стороны
 (3.2.5)
(3.2.5)
и с другой
 или
или  (3.2.6)
(3.2.6)
Этим условиям удовлетворяет, например, полуполоса  .Последовательные этапы её отображения изображены на рис. 3.2.2.
.Последовательные этапы её отображения изображены на рис. 3.2.2.

Рисунок 3.2.2.
Видно, что  в комплексной плоскости не ограничен. Например, в лучах
в комплексной плоскости не ограничен. Например, в лучах  , он принимает действительные значения, по модулю большие единицы.
, он принимает действительные значения, по модулю большие единицы.
Отметим, что в (замкнутой) полосе  функция
функция  принимает значение 0 лишь в точках
принимает значение 0 лишь в точках  и
и  . Учитывая нечетность и периодичность этой функции, отсюда можно заключить, что она обращается в 0 лишь на действительной оси в точках
. Учитывая нечетность и периодичность этой функции, отсюда можно заключить, что она обращается в 0 лишь на действительной оси в точках 
Заметим, что отображение  в силу соотношения
в силу соотношения  можно представлять, как только что рассмотренное, лишь со сдвигом.
можно представлять, как только что рассмотренное, лишь со сдвигом.
6. Гиперболические функции  и
и 
С тригонометрическими функциями тесно связаны гиперболические функции, определяемы посредством формул
 ,
, 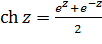 . (3.3.1)
. (3.3.1)
Эти функции всюду аналитичны. Они просто выражаются через тригонометрические функции:

 ,
,
то есть  ,
,  , и поэтому несущественно отличаются от них.
, и поэтому несущественно отличаются от них.
Дата добавления: 2015-08-17; просмотров: 1569 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Дробно-линейная функция | | | Сходимость аналитических функций |