Читайте также:
|
Пусть функция 
определена в некоторой окрестности точки 
.
Определение. Отображение 
называется конформным в точке , если оно сохраняет углы между кривыми и обладает свойством постоянства растяжений в точке .
Из выше сказанного вытекает, что если функция дифференцируема в некоторой окрестности точки (регулярна в точке ) и 
, то отображение является конформным в точке .
Определение. Пусть функция однолистна в области D и пусть отображение является конформным в каждой точке области D. Тогда это отображение называется конформным.
Если сохраняется не только величина углов, но и ориентация, то отображение называется конформным первого рода. Если же ориентация меняется на противоположную, то – конформным второго рода.
Из определения однолистной функции, определения конформного отображения в точке 
и свойств производной вытекает, что если функция
1. дифференцируема в области D,
2. однолистна в области D,
3. ее производная отлична от нуля в этой области,
то отображение является конформным.
Следующий материал готовить для доклада на следующем семинаре:
1. Линейная функция;
2. Дробно-линейнаяфункция;
3. Функция Жуковского.
4. Функция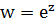 
;
5. Тригонометрические функции 
и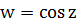 
;
6. Гиперболические функции 
и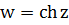 
.
Дата добавления: 2015-08-17; просмотров: 61 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Постоянство растяжений | | | Линейная функция |