
Читайте также:
|
Линейная функция является частным случаем функции вида:
 (2.2.1)
(2.2.1)
где 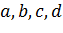 – комплексные число, при чем
– комплексные число, при чем  .
.
Функции вида (2.2.1) называются дробно-рациональными.
Дробно-линейную функцию можно распространять на всю расширенную комплексную плоскость.
Так как  , то точка
, то точка  переходит при этом отображении в
переходит при этом отображении в  , а точка
, а точка  в
в  .
.
Рассмотрим основные свойство дробно-линейных отображений.
1. Конформность.
Дробно линейная функция конформно отображает расширенную комплексную плоскость на расширенную комплексную плоскость.
Очевидно, что функция (2.2.1) регулярна во всей расширенной комплексной плоскость, за исключением точки  – полюса первого порядка. Решая уравнение (2.2.1) относительно
– полюса первого порядка. Решая уравнение (2.2.1) относительно  , находим функцию
, находим функцию
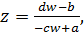 (2.2.2)
(2.2.2)
( ) обратную к функции (2.2.1).
) обратную к функции (2.2.1).
Функция (2.2.2) однозначна на всей расширенной комплексной плоскости и так же дробно-линейной. Следовательно, дробно-линейная функция однолистна в расширенной комплексной плоскости.
2. Групповое свойство.
Совокупность дробно-линейных отображений образует группу, т.е.
1)суперпозиция дробно-линейных отображений является дробно-линейным отображением.
2) Отображение, обратное к дробно-линейному, так же является дробно-линейным.
Докажем первое свойство. Пусть
 (2.2.3)
(2.2.3)
 (2.2.4)
(2.2.4)
Подставляя (2.2.3) в (2.2.4) получаем:
 где
где
 .
.
Второе свойство доказано в предыдущем пункте.
2. Круговое свойство.
При дробно-линейном отображении образом любой окружности или прямой является окружность или прямая.
Докажем это свойство. Сначала рассмотрим линейное отображение  . Это отображение сводится к подобию, повороту и переносу (пункт 1). Следовательно, линейное отображение переводит окружности в окружности, а прямые – в прямые.
. Это отображение сводится к подобию, повороту и переносу (пункт 1). Следовательно, линейное отображение переводит окружности в окружности, а прямые – в прямые.
В случае, когда дробно-линейная функция  не является линейной
не является линейной  , представим её в виде
, представим её в виде
 , (2.2.5)
, (2.2.5)
где  . Тогда отображение (2.2.5) сводится к последовательному выполнению следующих отображений:
. Тогда отображение (2.2.5) сводится к последовательному выполнению следующих отображений:
 (2.2.6)
(2.2.6)
Первое и третье отображения (2.2.6) обладают круговым свойством, так как они линейные. Остается доказать, что второе отображение (2.2.6), т.е. отображение
 , (2.2.7)
, (2.2.7)
так же обладает круговым свойством.
Уравнение любой окружности или прямой на плоскости  имеет вид
имеет вид
 (2.2.8)
(2.2.8)
(если  , то (3.2.9) – уравнение прямой).
, то (3.2.9) – уравнение прямой).
Так как 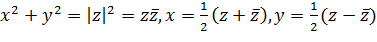 , то уравнение (2.2.8) записывается в виде
, то уравнение (2.2.8) записывается в виде
 , (2.2.9)
, (2.2.9)
где  .
.
Подставив в (2.2.9)  получаем
получаем
 . (2.2.10)
. (2.2.10)
Следовательно, образом окружности (2.2.9) (прямой, если  ) при отображении (2.2.7) является окружность (2.2.10) (прямая, если
) при отображении (2.2.7) является окружность (2.2.10) (прямая, если  ).
).
Отметим, что дробно-линейное отображение  переводит окружности и прямые, проходящие через точку
переводит окружности и прямые, проходящие через точку  в прямые, а остальные окружности и прямые – в окружности.
в прямые, а остальные окружности и прямые – в окружности.
Принято считать, что прямая – это окружность бесконечного радиуса. Поэтому коротко круговое свойство можно сформулировать так: при дробно-линейном отображении окружности переходят в окружности.
4. Свойство сохранения симметрии.
Понятие симметрии относительно окружности определяется в элементарной геометрии следующим образом. Пусть 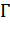 – окружность радиуса
– окружность радиуса 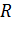 с центром в точке
с центром в точке 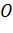 .
.
 |
 и
и  называются симметричными относительно окружности
называются симметричными относительно окружности 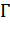 , если они лежат на одном луче, выходящем из точки
, если они лежат на одном луче, выходящем из точки 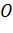 , и
, и  (Рис. 3.2.1).
(Рис. 3.2.1).
Рисунок 2.2.1.
В частности, каждая точка окружности 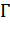 является симметричной сама себе относительно этой окружности.
является симметричной сама себе относительно этой окружности.
Таким образом, на комплексной плоскости точки  и
и  являются симметричными относительно окружности
являются симметричными относительно окружности  , если они лежат на одном луче, выходящем из точки
, если они лежат на одном луче, выходящем из точки  и
и  . Из этого определения вытекает, что симметричными относительно окружности
. Из этого определения вытекает, что симметричными относительно окружности  точки
точки  ,
,  связаны соотношением
связаны соотношением
 (2.2.11)
(2.2.11)
В частности, симметричные относительно единичной окружности  точки
точки  и
и  связаны соотношением:
связаны соотношением:
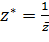 (2.2.12)
(2.2.12)
Так как точки  и
и 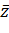 симметрично относительно действительной оси, то из (2.2.12) следует, что точка
симметрично относительно действительной оси, то из (2.2.12) следует, что точка  получается из точки
получается из точки  двойной симметрией: относительно действительной оси и относительно единичной окружность (в любом порядке).
двойной симметрией: относительно действительной оси и относительно единичной окружность (в любом порядке).
Из (2.2.11) вытекает, что симметричные относительно окружности  точки
точки  и
и  связаны соотношением
связаны соотношением
 (2.2.13).
(2.2.13).
Стоит отметить, что точки  и
и  являются симметричными относительно окружности
являются симметричными относительно окружности 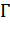 тогда и только тогда, когда любая окружность
тогда и только тогда, когда любая окружность  , проходящая через эти точки, пересекается с окружностью
, проходящая через эти точки, пересекается с окружностью 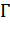 под прямым углом.
под прямым углом.
Дробно-линейное отображение обладает следующим свойством сохранения симметрии.
При дробно-линейном отображении пара точек, симметричных относительно окружности, переходит в пару точек, симметричных относительно образа этой окружности.
Здесь окружность, в частности, может быть прямой.
Докажем это свойство. Пусть точки  и
и  симметричны относительно окружности
симметричны относительно окружности 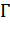 и пусть дробно-линейное отображение
и пусть дробно-линейное отображение 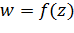 переводит окружность
переводит окружность 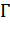 в
в  , а точки
, а точки  и
и  – в точки
– в точки 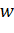 и
и  соответственно. В силу кругового свойства
соответственно. В силу кругового свойства  является окружностью. Нужно доказать, что точки
является окружностью. Нужно доказать, что точки 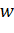 и
и  симметричны относительно
симметричны относительно  . Для этого достаточно доказать, что любая окружность
. Для этого достаточно доказать, что любая окружность 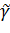 , проходящая через точки
, проходящая через точки 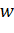 и
и  , пересекается с
, пересекается с  под прямым углом.
под прямым углом.
Прообразом окружности 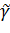 при дробно-линейном отображении
при дробно-линейном отображении 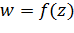 является окружность
является окружность  , проходящая через точки
, проходящая через точки  и
и  . Эта окружность
. Эта окружность  пересекается с
пересекается с 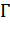 под прямым углом. Следовательно,
под прямым углом. Следовательно, 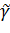 пересекается с
пересекается с  так же под прямым углом, так как дробно-линейное отображение является конформным во всей расширенной плоскости и сохраняет углы между кривыми в каждой точке.
так же под прямым углом, так как дробно-линейное отображение является конформным во всей расширенной плоскости и сохраняет углы между кривыми в каждой точке.
5. Дробно-линейное отображение, переводящее три точки в три точки.
Существует единственное дробно-линейное отображение, при котором три различные точки 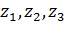 переходят в три различные точки
переходят в три различные точки 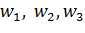 . Это отображение определяется формулой
. Это отображение определяется формулой
 (2.2.14)
(2.2.14)
Докажем это свойство. Из группового свойства следует, что функция 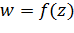 , определяемая соотношением (2.2.14), является дробно-линейной. Так же ясно, что
, определяемая соотношением (2.2.14), является дробно-линейной. Так же ясно, что 
Докажем, что если дробно-линейная функция  удовлетворяет тем же условиям, что и
удовлетворяет тем же условиям, что и 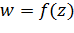 ,а именно
,а именно 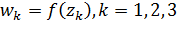 , то
, то  . Пусть
. Пусть 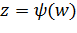 – функция, обратная функции
– функция, обратная функции 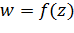 . Тогда
. Тогда  – дробно-линейная функция:
– дробно-линейная функция:
 и
и  . То есть
. То есть  ,
, 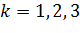
Отсюда получаем  ,то есть квадратное уравнение
,то есть квадратное уравнение 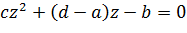 имеет три различных корня. Следовательно,
имеет три различных корня. Следовательно, 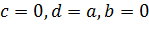 и
и 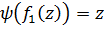 , откуда
, откуда  .Свойство доказано.
.Свойство доказано.
Заметим, что функция 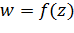 ,определенная формулой (3.2.15), конформно отображает круг, граница которого проходит через точки
,определенная формулой (3.2.15), конформно отображает круг, граница которого проходит через точки  ,
, 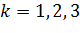 , на круг, граница которого проходит через точки
, на круг, граница которого проходит через точки 
Дата добавления: 2015-08-17; просмотров: 174 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Линейная функция | | | Функция Жуковского |