Читайте также:
|
Пусть функция 
дифференцируема в некоторой окрестности точки 
и 
. Рассмотрим произвольную точку 
кривой 
, расположенную достаточно близко к точке (рис. 2.1).
Рисунок 2.1.
Обозначим 
, 
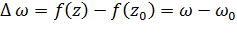. Из определения производной 
следует, что
, где 
при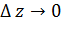 
,
откуда получаем
или
. (2.1).
Пусть 
, где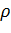 
достаточно мало, тогда из формулы (2.1) находим, что окружность 
переходит при отображении в кривую, которая мало отличается от окружности
.
Иначе говоря, отображение с точностью до малых более высокого порядка, чем 
, растягивает круг 
в 
раз.
Величина 
называется линейным растяжением кривой в точке при отображении . Следовательно, линейное растяжение в точке не зависит от вида и направления кривой и равно 
.
Дата добавления: 2015-08-17; просмотров: 76 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Сохранение угла между кривыми | | | Определение конформного отображения |