Линейная функция

Определение.Линейной функцией называется функция вида:

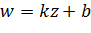, (1.1.)

где и – некоторые постоянные комплексные числа .

Очевидно, что отображение (1.1.) будет конформным во всей плоскости комплексного переменного и при том взаимно однозначным.

Рассмотрим сначала три случая, при чем, для простоты и 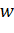будем изображать точками одной плоскости.

1) .

Это отображение есть сложение векторов, а, фактически, параллельный перенос точек плоскости на вектор 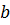.(Рис. 2.1.1).

Рисунок 2.1.1.

2) .

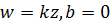Пусть 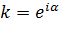, тогда 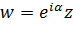. В этом случае имеем:

,

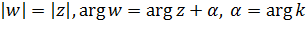то есть точка переходит в точку 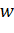при помощи вокруг поворота около нулевой точки на угол 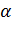. Значит, это отображение есть поворот вокруг начала координат на угол 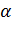(Рис. 2.1.2).

Рисунок 2.1.2.

3) – постоянное комплексное число (если , то все точки комплексной плоскости перейдут в нулевую точку).

Запишем в показательной форме, тогда получим

.

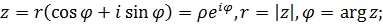
Это означает, что длина вектора меняется в 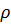раз (то есть 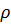– коэффициент подобия) и к аргументу прибавляется угол (поворот вокруг начала координат на угол ).

Окончательно получим, что отображение, осуществляемое функцией 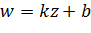, есть комбинация преобразований точек плоскости:

1. поворот вокруг начала координат на угол, равный аргументу числа ;

2. подобие с центром в начале координат и коэффициентом подобия 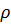равным модулю числа ;

3. параллельный перенос на вектор 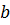, при котором начало координат переходит в точку .

Функция является аналитической.

При отображении, осуществляемом с помощью линейной функции, фигуры переходят в подобные им фигуры (на рис. 2.1.3. это показано для функции ). Это свойство называется свойством сохранения формы.

Рисунок 2.1.3.

Этим свойством обладает и преобразование 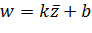, которое называется антилинейным. Оно сохраняет форму, но меняет ориентацию обхода границы фигуры на противоположную (На Рис. 2.1.4. это показано для функции )

Рисунок 2.1.4.

Отсюда вытекает, что любое преобразование подобия задается линейной или антилинейной функцией, при чем если ориентация сохраняется, то оно задается линейной функцией.

Поскольку линейная функция 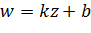определяется двумя параметрами и , то для её задания нужны два условия.

Дата добавления: 2015-08-17