Читайте также:
|
Пусть функция 
дифференцируема в некоторой окрестности точки 
и пусть 
. Рассмотрим гладкую кривую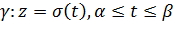 
(Рис. 1.1), проходящую через точку 
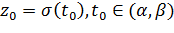. Обозначим 
угол, образуемый касательной к кривой 
, в точке и положительным направлением действительной оси (касательная считается направленной в ту же сторону, что и кривая). Тогда 
.
 |
Рисунок 1.2.
Пусть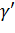 
— образ кривой при отображении , т. е. 
, а точка 
— образ точки 
. По правилу дифференцирования сложной функции
(1.1)
Так как по условию и 
, то 
, т. е. кривая 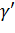имеет касательную в точке . Пусть 
. Тогда из (1.1) находим 
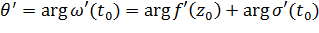, то есть
(1.2)
Величина 
называется углом поворота кривой в точке при отображении .
Из формулы (1.2) следует, что если , то угол поворота в точке не зависит от кривой и равен 
, т. е. все кривые, проходящие через точку , поворачиваются при отображении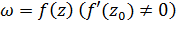 
на один и тот же угол, равный аргументу производной в точке .
Таким образом, отображение 
, где 
— дифференцируемая в окрестности точки функция и , сохраняет углы между кривыми, проходящими через точку , не только по величине, но и по направлению отсчета (рис. 1.2).
Дата добавления: 2015-08-17; просмотров: 56 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Геометрический смысл модуля и аргумента производной | | | Постоянство растяжений |