Сходимость аналитических функций

Лекция №2.

Теорема о логарифмическом вычете, принцип аргумента. Теорема Руше. Теорема Гурвица о пределе последовательностей аналитических функций. Определение вычета. Логарифмическая функция и логарифмический вычет. Кратность нуля и полюса для мероморфной функции.

Теоретические вопросы:

1) Сходимость последовательности аналитических функций;

2) Теорема Вейерштрасса;

3) Теорема Руше;

4) Теорема Гурвица;

Содержание лекции

Сходимость аналитических функций

Ранее было рассмотрено определение последовательности непрерывных функций. Для данной последовательности имеет место следующая теорема:

Теорема 2.1. Если функции непрерывны на множестве , то в случае равномерной сходимости их на к конечной функции ,последняя также непрерывна на .

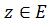Доказательство. Действительно, пусть ; для заданного существует такой номер , что для всех имеем . Далее, существует число такое, что для всех с имеем (возможно в силу непрерывности на ).

Отсюда для с имеем: ,что и означает непрерывность в точке .

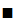
Отсюда далее следует, что если функции непрерывны в области и равномерно сходятся внутри к конечной функции то непрерывна в .

В случае аналитических функций имеет место следующая фундаментальная теорема Вейерштрасса.

Дата добавления: 2015-08-17