Читайте также:
|
Теорема 2.4. (теорема Руше). Пусть функции 
и 
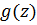регулярны в ограниченной односвязной области 
и на ее границе 
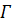и пусть для всех 
имеет место неравенство 
. Тогда функции и 
имеют в области одинаковое число нулей.
Доказательство. Используя теорему о логарифмическом вычете, отметим, что 
– количество нулей функции 
.
Обозначим величину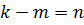 
. Функцию 
можно представить в следующем виде:
, где 
То есть 
, где 
– ноль функции , а 
– его порядок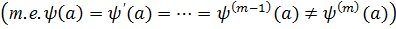 
.
Пусть 
, где – полюс 1-го порядка. Значит, 
1
Для 
.
Надо показать, что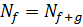 
. Пусть 
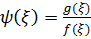. Тогда 
. Значит, 
.
Получаем:
Cдругой стороны, так как
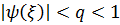и 
,
то 
..
Получается, что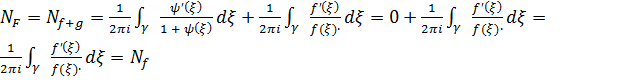 
, то есть 
. 
Относительно равномерно сходящихся последовательностей регулярных функций докажем еще следующую теорему, имеющую многочисленные применения.
Дата добавления: 2015-08-17; просмотров: 85 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Теорема о логарифмическом вычете | | | Теорема Гурвица |