Читайте также:
|
Теорема 2.3. (теорема о логарифмическом вычете). Пусть G – некая область комплексной плоскости. f – аналитическая функция в области G.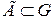 
- гладкий контур внутри G.
Пусть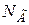 
- количество нулей функции f внутри Г (считая их кратность), тогда получим равенство:
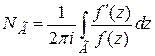. (1)
Доказательство. Используем теорему Коши о вычетах, согласно которой:
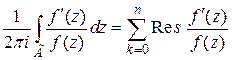. (2)
Пусть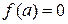 
порядка 
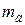. Разложим функцию:
.
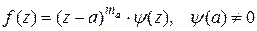Вычислим производную:
.
.
.
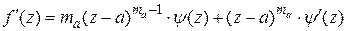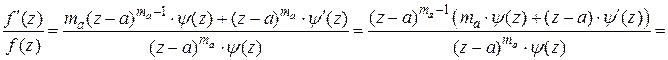
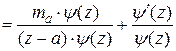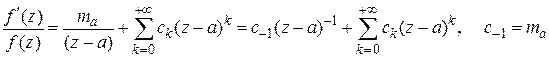Следовательно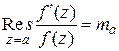 
, где 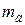- порядок нуля в точке а.
Отсюда следует, что:
. 
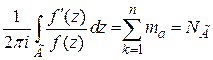При подсчете числа нулей регулярной функции в заданной области часто применяется теорема Руше.
Дата добавления: 2015-08-17; просмотров: 149 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Теорема Вейерштрасса | | | Теорема Руше |