Теорема Вейерштрасса

Теорема 2.2. (Вейерштрасса). Если последовательность функций , регулярных в области , равномерно сходится внутри к конечной функции то регулярна в и последовательность производных равномерно сходится внутри к .

Доказательство. Возьмем какой-либо замкнутый круг , лежащий в , и концентрический с ним замкнутый круг большего радиуса, также лежащий в . Если есть граница , то по формулам Коши имеем для :

(1)

С другой стороны, так как непрерывна в , то функция

(2)

будет регулярной в . Из (1) и (2) имеем для :

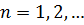(3)

и аналогично

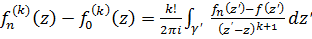(4)

Но на последовательность равномерно сходится и, следовательно, для заданного существует такое, что при на будет: .

Имея это в виду, из (3) и (4) получаем при

(5)

где и — радиусы кругов и .

Первое из этих неравенств показывает, что сходится в к функции , которая по условию должна совпадать с Следовательно, регулярна внутри . Но — любой круг, лежащий в . Поэтому регулярна в , если не содержит ∞.

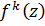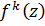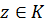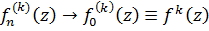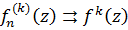Далее, второе из неравенств (5), если заменить в нем на , показывает, что последовательность равномерно сходится в к , так как, за счет выбора , правую часть можно сделать сколь угодно малой сразу для всех , то есть так как в , то в .

Чтобы доказать равномерную сходимость 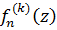внутри , отметим, что каждое ограниченное замкнутое множество можно покрыть конечным числом кругов, целиком лежащих в вместе с границами.

Действительно, для каждой точки существует замкнутый круг с центром в , лежащий в . Совокупность этих кругов (для всех ) целиком покрывает . По теореме Гейне — Бореля существует конечное число кругов, также покрывающих .

Пусть эти круги будут .

Тогда, по доказанному, для существуют 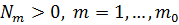, то при и имеем . Если есть наибольшее из чисел , то при неравенство имеет место для точек всех кругов , , 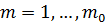а следовательно, и для всех , т. е. последовательность равномерно сходится на .

Дата добавления: 2015-08-17