Теорема Гурвица

Теорема 2.5. (Гурвица) Если последовательность функций , регулярных в области 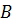, равномерно сходится внутри 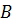к регулярной функции 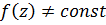и если каждая из функций принимает данное значение не более кем в 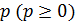точках области 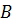, то и функция принимает значение не более кем в точках из .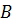

Доказательство. Пусть сначала 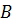не содержит ∞. Допустим, что принимает значение в различных точках Опишем около точек , столь малые окружности , чтобы они лежали внедруг друга, содержали внутри себя лишь точки области 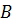и чтобы на них не было нулей функции .

Все это возможно выполнить, поскольку 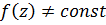. При этих условиях существует такое, что на всех окружностях имеем .

Так как последовательность функций равномерно сходится на окружностях , то существует такое, что на , , имеем . Из

по теореме Руше заключаем, что функция 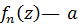внутри каждой окружности , наверное имеет нули, nтаккак их имеет функция .

Следовательно, принимает значение не менее, чем в точках области 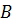, что противоречит условию теоремы.

Если область 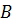содержит ∞, но отлична от полной плоскости, то, отобразив ее надлежащей дробно-линейной функцией на область, не содержащую ∞, можно применить к преобразованным функциям выше доказанное.

И случай, когда область 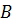является всей плоскостью , исключается, так как в этом случае всегда .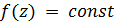

Следствие 2.2.1. Если последовательность однолистных функций сходится к функции , то является однолистной функцией, при чем .

Дата добавления: 2015-08-17