
Читайте также:
|
1) Объем тела, полученного в результате вращения графика функции y=f(x), ограниченной линиями x=a и x=bвокруг оси Ох вычисляется по формуле:
V= 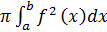
2) Объем тела, полученного в результате вращения графика функции y=f(x), ограниченной линиями y=cи y=dвокруг оси Оу вычисляется по формуле:
3) V= 
Длина кривой y=f(x) в отрезке [a,b]


Дата добавления: 2015-08-17; просмотров: 69 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ИНТЕГРАЛ | | | Основные свойства призвольного труегольника |