Вязкий поток

Перейдем теперь к общей теории вязкого потока, по крайней мере настолько общей, насколько это и известно человеку. Вы уже понимаете, что компоненты сдвиговых напряжений сдвига пропорциональны пространственным производным от раз­личных компонент скорости, таких, как dv_x/dy или dv_y/дх. Однако в общем случае сжимаемой жидкости в напряжениях есть и другой член, который зависит от других производных скорости. Общее выражение имеет вид

где х_i — какая-либо из координат х, у или z; v_i — какая-либо з прямоугольных составляющих скорости. (Значок d_ij обозна­чает символ Кронекера, который равен единице при i=j и нулю при i¹j.) Ко всем диагональным элементам S_ij тензора напряжений прибавляется дополнительный член h'Ñ•v. Если жидкость несжимаема, то Ñ•v=0 и дополнительного члена не появляется, так что он действительно имеет отношение к внутренним силам при сжатии. Для описания жидкости, точно так же как и для описания однородного упругого тела, требуются две постоянные. Коэффициент h представляет «обыч­ный» коэффициент вязкости, который мы уже учитывали. Он называется также первым коэффициентом вязкости, а новый коэффициент h' называется вторым коэффициентом вязкости.

Теперь нам предстоит найти вязкую силу f _вязк, действую­щую на единицу объема, после чего мы сможем подставить ее в уравнение (41.1) и получить уравнение движения реальной жидкости. Сила, действующая на маленький кубический объем жидкости, представляет собой равнодействующую всех сил, действующих на все шесть граней. Взяв их по две сразу, мы получим разность, которая зависит от производных напряжений, и, следовательно, от вторых производных скоростей. Это прият­ный результат, ибо он приведет нас опять к векторному урав­нению. Компонента вязкой силы, действующей на единицу объема в направлении оси х_i, равна

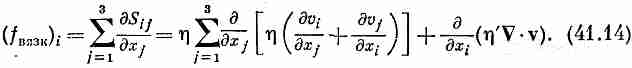
Обычно зависимость коэффициентов вязкости от координат положения несущественна и ею можно пренебречь. Тогда вяз­кая сила на единицу объема содержит только вторые производ­ные скорости. Мы видели в гл. 39, что наиболее общей формой вторых производных в векторном уравнении будет сумма Лапласиана (Ñ•Ñ)v = Ѳv и градиента дивергенции (Ñ (Ñ•v)). Выражение (41.14) представляет как раз такую сумму с коэф­фициентами h и ( h+h'). Мы получаем

В случае несжимаемой жидкости Ñ•v=0 и вязкая сила в еди­нице объема будет просто равна hѲv. Это и все, чем обычно пользуются; однако если вам понадобится вычислить погло­щение звука в жидкости, то вам потребуется и второй член. Теперь мы можем закончить вывод уравнения движения реальной жидкости. Подставляя (41.15) в уравнение (41.1), получаем

Уравнение получилось, конечно, сложное, но ничего не поде­лаешь, такова природа.

Если мы введем W=ÑXv, как делали это раньше, то наше уравнение можно записать в виде

Мы снова предполагаем, что единственными объемными силами являются консервативные силы типа сил тяжести. Чтобы понять смысл нового члена, давайте рассмотрим случай несжимаемой жидкости. Если мы возьмем ротор уравнения (41.16), то полу­чим

Это напоминает (40.9) с той только разницей, что в правой части имеется еще одно слагаемое. Когда правая часть была равна нулю, то имелась теорема Гельмгольца о том, что вихри всегда движутся вместе с жидкостью. Теперь же в правой части появилось довольно сложное выражение, из которого, однако, не сразу же следуют физические выводы. Если бы мы пренебрегли членом ÑX(WXv), то получили бы диффузион­ное уравнение. Новый член означает, что вихри диффундируют в жидкости. При большом градиенте вихри расползаются в со­седние области жидкости.

Именно поэтому утолщаются кольца табачного дыма. С этим же связано красивое явление, возникающее при прохождении кольца «чистого» вихря (т. е. «бездымного» кольца, созданного с помощью описанной в предыдущей главе аппаратуры) через облако дыма. Когда оно выходит из облака, к нему «прилипает» некое количество дыма и мы видим полую оболочку из дыма. Какое-то количество завихренности W диффундирует в окру­жающий дым, продолжая свое движение вперед вместе с вихрем.

Дата добавления: 2015-08-20