Тензор упругости

Теперь, чтобы описать деформации, мы должны связать их с внутренними силами — с напряжениями в материале. Мы предполагаем, что закон Гука справедлив для любого кусочка материала, т. е. что напряжения всюду пропорциональны дефор­мациям. В гл. 31 мы определили тензор напряжений S_ij как i-ю компоненту силы, действующей на единичной площадке, перпендикулярной оси j. Закон Гука говорит, что каждая ком­понента S_ijлинейно связана с каждой компонентой напряжения. Но поскольку S и l содержат по девяти компонент, то всего для описания упругих свойств материала требуется 9X9=81 возможный коэффициент. Если материал однороден, то все эти коэффициенты будут постоянными. Мы обозначим их C _ijkl определив посредством уравнения

где каждый значок i, j, k и l может принимать значения 1, 2 или 3. Поскольку коэффициенты С_ijkl связывают один тензор с другим, они тоже образуют тензор — на этот раз тензор четвертого ранга. Мы можем назвать его тензором упругости.

Предположим, что все C _ijkl известны и что к телу какой-то произвольной формы мы приложили сложные силы. При этом возникнут все сорта деформаций — тело как-то исказится. Каковы будут перемещения? Вы понимаете, что это довольно сложная задача. Если вам известны деформации, то из уравне­ния (39.12) можно найти напряжения, и наоборот. Но напряже­ния и деформации, которые возникли в любой точке, зависят от того, что происходит во всей остальной части материала.

Наиболее простой способ подступиться к такой задаче — это подумать об энергии. Когда сила F пропорциональна пере­мещению х, скажем F=kx, то работа, затраченная на любое перемещение х, равна kx²/2. Подобным же образом энергия w, запасенная в любой единице объема деформированного мате­риала, оказывается равной

Полная же работа W, затраченная на деформацию всего тела, будет интегралом от w по всему его объему:

Следовательно, это и есть потенциальная энергия, запасенная во внутренних напряжениях материала. Когда тело находится в равновесии, эта внутренняя энергия должна быть минималь­ной. Таким образом, проблема определения деформаций в теле может быть решена нахождением таких перемещений и по всему телу, при которых W минимальна. В гл. 19 (вып. 6) я го­ворил вам о некоторых общих идеях вариационного исчисле­ния, применяемого при решении задач на минимизацию подоб­ного рода. Однако сейчас мы больше не будем вдаваться в под­робности этой задачи.

Сейчас нас главным образом будет интересовать то, что можно сказать относительно общих свойств тензора упругости. Прежде всего ясно, что на самом деле в C_ijkl содержится не 81 различный параметр. Поскольку S_ij и e_ij — симметричные тензоры, каждый из которых включает только шесть различных элементов, то C _ijkl состоит максимум из 36 различных компо­нент. Обычно же их гораздо меньше.

Рассмотрим специальный случай кубического кристалла. Плотность энергии w для него получается такой:

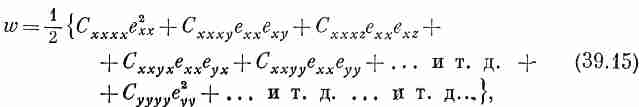
т. е. всего 81 слагаемое! Но кубический кристалл обладает определенными симметриями. В частности, если кристалл по­вернуть на 90°, то все его физические свойства останутся теми же. Например, у него должна быть одна и та же жесткость относительно растяжения как в направлении оси у, так и в нап­равлении оси х. Следовательно, если мы переменим наши опре­деления осей координат х и у в уравнении (39.15), то энергия не должна измениться. Поэтому для кубического кристалла

C_хххх = С_уууу=C_zzzz. (39.16)

Мы можем еще показать, что компоненты, наподобие С_ххху, должны быть нулями. Кубический кристалл обладает тем свой­ством, что он симметричен при отражении относительно любой плоскости, перпендикулярной к одной из осей координат. Если мы заменим у на —y, то ничего не должно измениться. Но из­менение у на - у меняет е_xy на - е_xy, так как перемещение в нап­равлении + у будет теперь перемещением в направлении - у. Чтобы энергия при этом не менялась, С_ххху должно переходить в - С_ххху Но отраженный кристалл будет тем же, что и прежде, поэтому С_ххxy должно быть таким же, как и - С_ххху. Это может произойти только тогда, когда оба они равны нулю.

Но вы можете сказать: «Рассуждая таким же образом, можно сделать и C _yyyy =0! » Это неверно. Ведь здесь у нас четыре игрека. Каждый у изменяет знак, а четыре минуса дают плюс. Если у встречается два или четыре раза, то такие компоненты не должны быть равны нулю. Нулю равны только те компо­ненты, у которых у встречается либо один, либо три раза. Таким образом, для кубического кристалла не равны нулю только те С, у которых один и тот же значок встречается четное число раз. (Рассуждения, которые мы провели для у, имеют силу и для х и для z.) Таким образом, выживают только компоненты типа С_ххуу, С_хуху, С_хуух и т. д. Однако мы уже показали, что если изменить все х на у и наоборот (или все z на x и т. д.), то для кубического кристалла мы должны получить то же самое число. Это означает, что остаются всего три различные ненуле­вые возможности:

Плотность же энергии для кубического кристалла выглядит так:

У изотропного, т. е. некристаллического, материала симмет­рия еще выше. Числа С должны быть теми же самыми при любом выборе осей координат. При этом, как оказывается, существует другая связь между коэффициентами С:

C_хххх=C_ххуу+C_хуху (39.19)

Это можно усмотреть из следующих общих рассуждений. Тен­зор напряжений S_ij должен быть связан с e_ij способом, который совершенно не зависит от направления осей координат, т. е. он должен быть связан только с помощью скалярных величин. «Это очень просто»,— скажете вы. «Единственный способ полу­чить S_ij из e_ij — умножить последнее на скалярную постоянную. Получится как раз закон Гука: S_ij= (Постоянная)Xе_ij». Однако это не совсем верно. Дополнительно здесь можно вста­вить единичный тензор d_ij, умноженный на некоторый скаляр, линейно связанный с е_ij. Единственный инвариант, который можно составить и который линеен по е, — это Se _jj. (Он преоб­разуется подобно х² +y²+z², а значит является скаляром.) Таким образом, наиболее общей формой уравнения, связывающего S_ij с e_ij для изотропного материала, будет

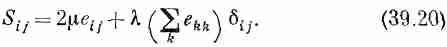
(Первая константа обычно записывается как 2m; при этом коэффициенту равен модулю сдвига, определенному нами в пре­дыдущей главе.) Постоянные (m, и l называются упругими по­стоянными Лямэ. Сравнивая уравнения (39.20) с уравнением (39.12), вы видите, что

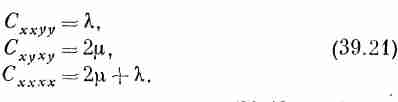
Таким образом, мы доказали, что уравнение (39.19) действи­тельно правильное. Вы видите также, что упругие свойства изотропного материала, как уже говорилось в предыдущей главе, полностью задаются двумя постоянными.

Коэффициенты С могут быть выражены через любые две из упругих постоянных, которые использовались ранее, напри­мер через модуль Юнга Y и отношение Пуассона s. На вашу долю оставляю показать, что

Дата добавления: 2015-08-20