Движения в упругом теле

Мы подчеркивали, что в упругом теле, находящемся в равно­весии, внутренние напряжения распределяются так, чтобы энергия была минимальной. Посмотрим теперь, что происходит, если внутренние силы не уравновешены. Возьмем маленький кусочек материала внутри некоторой поверхности А (фиг. 39.5).

Фиг. 39.5. Маленький элемент объема V, ограниченный поверхностью А,

Если этот кусочек находится в равновесии, то полная действую­щая на него сила F должна быть равна нулю. Можно считать, что эта сила состоит из двух частей, одна из которых обуслов­лена «внешними» силами, подобными гравитации, действующими на расстоянии на вещество нашего кусочка и приводящими к величине силы на единицу объема f _внешн. Полная же внешняя сила F _внешн равна интегралу от f _внешн по всему объему кусочка:

В равновесии эти силы балансируются полной силой F _внутр, действующей по поверхности А со стороны окружающего материала. Когда же этот кусочек не на­ходится в равновесии, а движется, сум­ма внутренних и внешних сил будет равна произведению массы на ускорение. При этом мы получаем

где r—плотность материала, а ŕ — его ускорение. Теперь мы можем скомбинировать уравнения (39.23) и (39.24) и написать

Нашу запись можно упростить, положив

Тогда уравнение (39.25) запишется в виде

Величина, названная нами F _внутр, связана с напряжениями в материале. Тензор напряжений S_ij был определен нами в гл. 31 таким образом, что x-компонента силы dF, действующей на эле­мент поверхности da с нормалью n, задается выражением

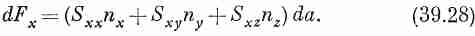
Отсюда х-компонента силы F _внутр, действующей на наш ку­сочек, равна интегралу от dF_x по всей поверхности. Подстав­ляя это в x-компоненту уравнения (39.27), получаем

Оказалось, что поверхностный интеграл связан с интегра­лом по объему, а это напоминает нам нечто знакомое по главам об электричестве. Заметьте, что если не обращать внимания на первый значок х в каждом из S в левой части (39.29), то она выг­лядит в точности как интеграл от величины (S•n), т.е. нормаль­ной компоненты вектора по поверхности. Она была бы равна потоку S через объем. А используя теорему Гаусса, поток можно было бы записать в виде объемного интеграла от дивергенции S. На самом деле все это справедливо независимо от того, есть ли у нас индекс х или нет. Это просто математическая теорема, которая доказывается интегрированием по частям. Другими словами, уравнение (39.29) можно превратить в

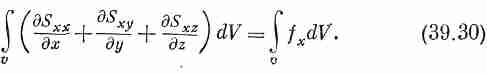
Теперь можно отбросить интегралы по объему и написать дифференциальное уравнение для любой компоненты f:

Оно говорит нам, как связана сила, действующая на единицу объема с тензором напряжения S_ij.

Вот как работает эта теория внутренних движений твердого тела. Если первоначально нам известны перемещения, задавае­мые, скажем, вектором и, то можно найти деформации e_ij. Из деформаций с помощью уравнения (39.12) можно получить напряжения. Затем с помощью уравнения (39.31) мы из напряжений можем найти плотности сил f. А зная f, мы из уравнения (39.26) получаем ускорение r в материале, которое подскажет нам, как изменятся перемещения. Собирая все это вместе, мы получаем ужасно сложные уравнения движения упругого твердого тела. Я просто напишу вам ответ для изо­тропного материала. Если вы воспользуетесь для S_ij уравне­нием (39.20) и запишете e_ij в виде ¹/₂ (du_i/dx_j+du_j]dx_i), то окончательно получите векторное уравнение:

Вы можете очень просто убедиться в том, что уравнение должно иметь такую форму. Сила должна зависеть от второй производной — перемещения и. Но какие можно составить вторые производные и так, чтобы они были векторами? Одна из них Ñ (Ñ•u); это самый настоящий вектор. Есть еще только одна такая комбинация — это Ѳu. Так что наиболее общей формой силы будет

что как раз дает (39.32) с другим определением постоянных. Вас может удивить, почему у нас нет третьего слагаемого ÑXÑXu, которое тоже вектор. Но вспомните, что ÑXÑXu

в точности равно Ѳu-Ñ(Ñ•u), т. е. это линейная комбина­ция двух уже написанных слагаемых. Так что оно не добавит ничего нового. Мы еще раз доказали, что в изотропном мате­риале есть только две упругие постоянные.

Для получения уравнения движения материала мы можем положить выражение (39.32) равным r д² u /дt² и, пренебрегая объемными силами типа силы тяжести, написать

Это уравнение выглядит похожим на волновое уравнение, с которым мы познакомились в электромагнетизме, за исклю­чением одного добавленного слагаемого, которое усложняет дело. Для материалов, упругие свойства которых всюду оди­наковы, мы можем увидеть, на что похоже общее решение. Вы, наверное, помните, что любое векторное поле может быть записано в виде суммы двух векторов, у одного из которых нулю равна дивергенция, а у другого — ротор. Другими сло­вами, можно положить

где

Подставляя вместо u в уравнении (39.33) u ₁+ u ₂, получаем

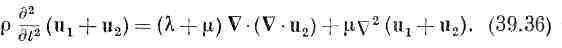
Взяв дивергенцию этого уравнения, мы можем исключить из него u₁:

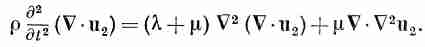
Поскольку операторы Ѳ и Ñ могут быть переставлены, можно вынести оператор дивергенции и получить

А так как ÑX u ₂, по определению, равно нулю, то ротор вы­ражения в фигурных скобках также будет нулем, так что выражение в скобках само по себе тождественно равно нулю и

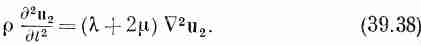
Это векторное волновое уравнение для волн, движущихся со скоростью С₂ = Ö(l+2m)/r. Поскольку ротор u ₂ есть нуль, то эти волны не связаны со сдвигом, а представляют просто волны сжатия наподобие звуковых, которые мы изучали в предыдущих главах и скорость которых как раз равна найденной нами для С_прод.

Подобным же образом, беря ротор уравнения (39.36), можно показать, что u ₁ удовлетворяет уравнению

Это снова векторное волновое уравнение для волн, распро­страняющихся со скоростью C₂ =Öm/r. Поскольку Ñ• u ₁ равно нулю, то перемещение u₁ не приводит к изменению плот­ности; вектор u₁ соответствует поперечным или сдвиговым волнам, которые встречались нам в предыдущей главе, а

C₂=C_сдвиг.

Если мы хотим знать статические напряжения в изотропном материале, то в принципе их можно найти, решая уравнение (39.32) с f, равным нулю (или равным статическим объемным силам, обусловленным силой тяжести, такой, как rg) при опре­деленных условиях, связанных с силами, действующими на поверхности нашего большого куска материала. Сделать это не­сколько сложнее, чем в соответствующих задачах электромагне­тизма. Во-первых, это более трудно потому, что сами уравнения несколько сложнее, и, во-вторых, формы тех упругих тел, кото­рыми мы обычно интересуемся, гораздо сложнее. На лекциях по электричеству мы часто интересовались решением уравнений Максвелла в областях сравнительно простой геометрической формы, таких, как цилиндр, сфера и т. д. В теории упру­гости, нам приходится заниматься объектами гораздо более сложной формы, например крюком подъемного крана, или ко­ленчатым автомобильным валом, или ротором газовой турбины. Такие задачи иногда можно приближенно решить численным методом, воспользовавшись принципом минимальной энер­гии, о котором мы упомянули ранее. Другой способ — это воспользоваться моделями предметов и измерять внутренние напряжения экспериментально с по­мощью поляризованного света.

Метод этот состоит в следующем. Когда кусок упругого изотропного ма­териала, например прозрачную пластмассу типа плекси­гласа, подвергают напряжению, в ней возникает двойное лучепреломление. Если пропускать через эту пластмассу поля­ризованный свет, то плоскость поляризации повернется на ве­личину, связанную с напряжением. Измеряя угол плоскости поляризации, можно измерить напряжение. На фиг. 39.6 пока­зан примерный вид этого устройства, а на фиг. 39.7 приведена фотография упругой модели сложной формы под напряжением.

Фиг. 39.6. Измерение внутренних напряжений с помощью поляризован­ного света.

Фиг. 39.7. Вид напряженной пластмассовой модели между двумя скрещенными полярои­дами.

Дата добавления: 2015-08-20