Кручение стержня; волны сдвига

Обратимся теперь к более сложному примеру, когда различ­ные части материала напряжены по-разному. Рассмотрим скру­ченный стержень — скажем, приводной вал какой-то машины или подвеску из кварцевой нити, применяемую в точных при­борах. Из опытов с маятником кручения вы, по-видимому, знае­те, что момент сил, действующий на закручиваемый стержень, пропорционален углу, причем константа пропорциональности, очевидно, зависит от длины стержня, его радиуса и свойств ма­териала. Но каким образом — вот в чем вопрос? Теперь мы в состоянии ответить на него: просто нужно немного разобраться в геометрии.

На фиг. 38.9, а показан цилиндрический стержень, облада­ющий длиной L и радиусом а, один из концов которого закручен на угол j по отношению к другому.

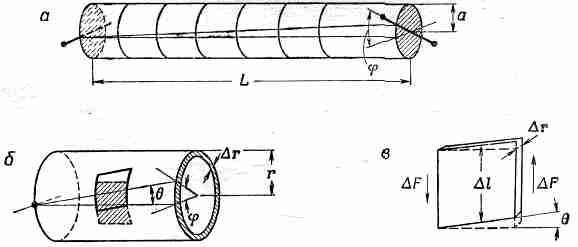
Фиг. 38.9. Кручение цилиндрического стержня (а), кручение цилин­дрического слоя (б) и сдвиг любого маленького кусочка в слое (в).

Если мы хотим связать де­формацию с тем, что уже известно, то стержень можно предста­вить состоящим из множества цилиндрических оболочек и выяснить, что происходит в каждой из этих оболочек. Начнем с рассмотрения тонкого короткого цилиндра радиусом r(мень­шего, чем в) и толщиной Dr, как показано на фиг. 38.9, б. Если теперь посмотреть на кусочек внутри этого цилиндра, который первоначально был маленьким квадратом, то можно заметить, что он превратился в параллелограмм. Каждый элемент ци­линдра сдвигается, а угол сдвига q равен

q=rj/L.

Поэтому напряжение сдвига g в материале будет [из уравне­ния (38.13)]

Напряжение среза равно тангенциальной силе DF, дейст­вующей на конец квадратика, поделенной на его площадь Dl/Dr (см. фиг. 38.9, б):

g=DF/DlDr.

Сила DF, действующая на конец такого квадратика, создает относительно оси стержня момент сил Dt, равный

Dt=rDF=rgDlDr. (38.22)

Полный момент t равен сумме таких моментов по всему периметру цилиндра. Складывая достаточное число таких кусков так, чтобы все Dl составляли 2pr, находим, что полный момент сил для пустотелой трубы равен

гg(2pr)Dr. (38.23)

Или, используя уравнение (38.21),

Мы получили, что жесткость t/j пустотелой трубы по отноше­нию к кручению пропорциональна кубу радиуса r и толщине Dr и обратно пропорциональна его длине L.

Теперь представьте себе, что стержень сделан из целой се­рии таких концентрических труб, каждая из которых закруче­на на угол j (хотя внутренние напряжения в каждой трубе раз­личны). Полный момент равен сумме моментов, требуемых для скручивания каждой оболочки, так что для твердого стержня

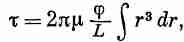
где интеграл берется от 0 до а — радиуса стержня. После ин­тегрирования получаем

Если закручивать стержень, то его момент оказывается про­порциональным углу и четвертой степени диаметра: стержень вдвое большего радиуса в шестнадцать раз жестче относительно кручения.

Прежде чем расстаться с кручением, рассмотрим применение теории к одной интересной задаче — волнам кручения. Возьмем длинный стержень и неожиданно закрутим один его конец; вдоль стержня, как показано на фиг. 38.10, а, пойдет волна кручения.

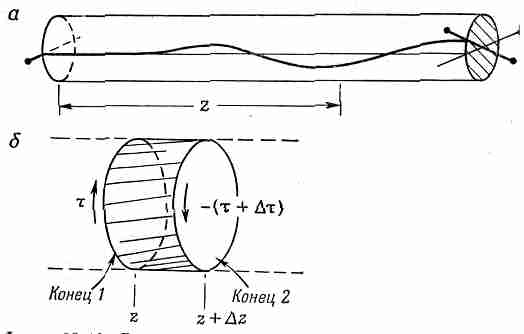
Фиг. 38.10. Волна кручения в стержне (а) и элемент объема стержня (б).

Это явление более интересно, нежели простое стати­ческое скручивание. Посмотрим, можем ли мы понять, как это происходит.

Пусть z — расстояние от некоторой точки до основания стержня. Для статического закручивания момент сил на всем протяжении стержня один и тот же и пропорционален j /L — полному углу вращения на полную длину. Но в нашей задаче важна местная деформация кручения, которая, как вы сразу поймете, равна дj/дz. Если кручение вдоль стержня неравно­мерное, то уравнение (38.25) следует заменить таким:

Посмотрим теперь, что же происходит с элементом длины Dz, который показан в увеличенном масштабе на фиг. 38.10, б. На конце 1 маленького отрезка стержня действует момент t(z), а на конце 2— другой момент сил t(z+Dz). Если величина Dz достаточно мала, то можно воспользоваться разложением в ряд Тэйлора и, сохранив только два члена, написать

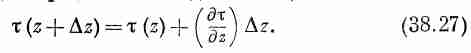
Полный момент сил Dt, действующий на маленький от­резок стержня между z и Dz, равен разности t(z) и

t(z+Dz),

или

Dt=(дt / д z)Dz.

Дифференцируя уравнение (38.26), получаем

Действие этого полного момента должно вызвать угловое ускорение отрезка стержня. Масса его равна

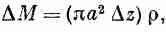
где r — плотность материала. В гл. 19 (вып. 2) мы нашли, что момент инерции кругового цилиндра равен mr²/2; обо­значая момент инерции нашего отрезка через Dl, получаем

Закон Ньютона говорит нам, что момент силы равен произ­ведению момента инерции на угловое ускорение, или

Дата добавления: 2015-08-20