Электромагниты

Поговорим теперь о практической стороне дела, которая немного более сложна. Предположим, что мы имеем электро­магнит стандартной формы, изображенный на фиг. 36.10.

Фиг. 36.10. Электромагнит.

Он состоит из С-образного железного ярма, на которое намотано много витков провода. Чему равно магнитное поле В в зазоре?

Если ширина зазора мала по сравнению со всеми другими размерами, то в качестве первого приближения мы можем счи­тать, что линии В образуют замкнутые кривые так же, как это происходит и в обычном торе. Они выглядят примерно так, как показано на фиг. 36.11,а.

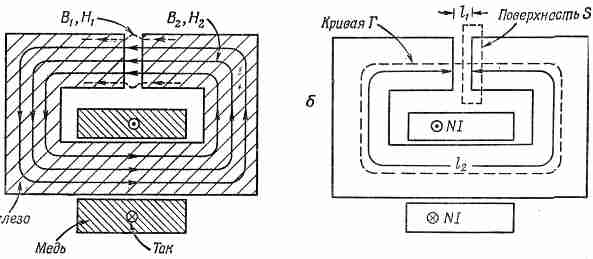
Фиг. 36.11. Поперечное сечение электромагнита.

Они стремятся вылезть из зазора, но если он узок, то эффект этот очень мал. Предположение о постоянст­ве потока В через любое попереч­ное сечение ярма будет довольно хорошим приближением. Если поперечное сечение ярма ме­няется равномерно и если мы пренебрежем любыми краевыми эффектами на зазоре или на углах, то можно говорить, что по всей окружности ярма В однородно.

Поле В в зазоре будет по величине тем же самым. Это следу­ет из уравнений (36.16). Представьте себе замкнутую поверх­ность S (см. фиг. 36.11,б), одна грань которой находится в зазоре, а другая — в железе. Полный поток поля В через эту поверхность должен быть равен нулю. Обозначая через В₁ величину поля в зазоре, а через B₂ — величину поля в железе, мы видим, что

B₁A₁-В₂А₂=0,

а поскольку А₁=А₂, то отсюда следует, что В₁=В₂.

Посмотрим теперь на Н. Мы снова можем воспользоваться уравнением (36.19), взяв криволинейный интеграл по контуру Г (см. фиг. 36.11,6). Как и прежде, правая часть равна NI — произведению числа витков на ток. Однако теперь Н в железе и в воздухе будет различным. Обозначая через Н₂ поле в железе, а через l ₂ — Длину пути по окружности ярма, мы видим, что эта часть кривой дает вклад в интеграл H₂l₂. Если же поле в зазоре равно Н₁, а ширина его l₁, то вклад зазора оказывается равным H₁l₁. Таким образом, получаем

Но это еще не все. Нам известно еще, что намагниченность в воздушной щели пренебрежимо мала, так что B₁=H₁. А так как B₁=B₂, то уравнение (36.26) принимает вид

Остаются еще два неизвестных. Чтобы найти В₂ и H₂, необхо­димо еще одно соотношение, которое связывает В с H в железе.

Если можно приближенно считать, что B₂=mH₂, то уравнение разрешается алгебраически. Рассмотрим более общий случай, для которого кривая намагничивания железа имеет вид, изоб­раженный на фиг. 36.8. Единственное, что нам нужно,— это найти совместное решение этого функционального соотношения с уравнением (36.27). Его можно найти, строя зависимость (36.27) на одном графике с кривой намагничивания, как это сделано на фиг. 36.12. Точки, где эти кривые пересекутся, и будут нашими решениями.

Для данного тока I уравнение (36.27) описывается прямой линией, обозначенной I >0 на фиг. 36.12. Эта линия пересекает ось Н (B₂=0) в точке H₂=NI/e₀c²l₂ и имеет наклон - l₂/l₁ Различные величины токов приводят просто к горизонтальному сдвигу этой линии. Из фиг. 36.12 мы видим, что при данном токе существует нес­колько различных решений, зависящих от того, каким об­разом вы получили их.

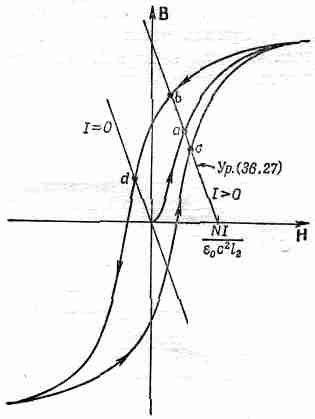
Фиг. 36.12. Определение поля в электромагните.

Если вы только что построили маг­нит и включили ток /, то поле B₂ (которое равно B₁) будет иметь величину, определяе­мую точкой а. Если вы сначала увеличили ток до очень большой величины, а затем пони­зили до I, то значение поля будет определяться точкой b. А если, увеличивая ток от большого отрицательного значения, вы до­шли до /, то поле определяется точкой с. Поле в зазоре зависит от того, как вы поступали в прошлом.

Если ток в магните равен нулю, то соотношение между В₂ и H₂ в уравнении (36.27) изображается кривой, обозначенной I =0 на фиг. 36.12. Здесь опять возможны различные решения. Если вы первоначально «насытили» железо, то в магните может сохраниться значительное остаточное поле, определяемое точ­кой d. Вы можете снять обмотку и получить постоянный маг­нит. Нетрудно понять, что для хорошего постоянного магнита необходим материал с широкой петлей гистерезиса. Такую очень широкую петлю имеют специальные сплавы, подобные Алнико V.

Дата добавления: 2015-08-20