Спонтанная намагниченность

Обратимся теперь к вопросу, почему в ферромагнитных мате­риалах даже малые магнитные поля приводят к такой большой намагниченности. Намагниченность ферромагнитных материа­лов типа железа или никеля образуется благодаря магнитным моментам электронов одной из внутренних оболочек атома. Магнитный момент mкаждого электрона равен произведению q/2m на g-фактор и момент количества движения J. Для отдель­ного электрона при отсутствии чисто орбитального движения g=2, а компонента J в любом направлении, скажем, в направ­лении оси z, равна ±h/2, так что компонента m в направлении оси z будет

m_z=gh/2m=0,928•10^-23 а/м ². (36.28)

В атоме железа вклад в ферромагнетизм фактически дают толь­ко два электрона, так что для упрощения рассуждений мы будем говорить об атоме никеля, который является ферромагнетиком, подобно железу, но имеет на той же внутренней оболочке только один «ферромагнитный» электрон. (Все рассуждения нетрудно затем распространить и на железо.)

Все дело в том, что точно так же, как и в описанных нами парамагнитных материалах, атомные магнитики в присутствии внешнего магнитного поля В стремятся выстроиться по полю, но их сбивает тепловое движение. В предыдущей главе мы вы­яснили, что равновесие между силами магнитного поля, стара­ющимися выстроить атомные магнитики, и действием теплового движения, стремящегося их сбить, приводит к тому, что сред­ний магнитный момент единицы объема в направлении В оказывается равным

где под В_а мы подразумеваем поле, действующее на атом, а под kT — тепловую (больцмановскую) энергию. В теории парамаг­нетизма мы в качестве В_а использовали само поле В, пренебре­гая при этом частью поля, действующего на каждый атом со стороны соседнего. Но в случае ферромагнетиков возникает усложнение. Мы уже не можем в качестве поля В_а, действующе­го на индивидуальный атом, брать среднее поле в железе. Вмес­то этого нам следует поступить так же, как это делалось в случае диэлектрика: нам нужно найти локальное поле, действующее на отдельный атом. При точном решении нам следовало бы сло­жить вклады всех полей от других атомов кристаллической решетки, действующих на рассматриваемый нами атом. Но по­добно тому как мы поступали в случае диэлектрика, сделаем приближение, состоящее в том, что поле, действующее на атом, будет таким же, как и в маленькой сферической полости внутри материала (предполагая при этом, как и раньше, что моменты соседних атомов не изменяются из-за наличия полости).

Следуя рассуждениям гл. 11 (вып. 5), мы можем надеяться, что должна получиться формула

похожая на формулу (11.25). Но это будет неправильно. Однако мы все же можем использовать полученные там результаты, если тщательно сравним уравнения из гл. 11 с уравнениями ферромагнетизма, которые мы напишем сейчас. Сопоставим сначала соответствующие исходные уравнения. Для областей, в которых токи проводимости и заряды отсутствуют, мы имеем:

Эти два набора уравнений можно считать аналогичными, если мы чисто математически сопоставим

Это то же самое, что и

Другими словами, если уравнения ферромагнетизма записать как

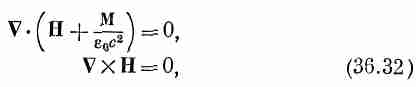
то они будут похожи на уравнения электростатики.

В прошлом это чисто алгебраическое соответствие доста­вило нам некоторые неприятности. Многие начинали думать, что именно Н и есть магнитное поле. Но, как мы уже убеди­лись, физически фундаментальными полями являются Е и В, а поле Н — понятие производное. Таким образом, хотя уравне­ния и аналогичны, физика их совершенно различна. Однако это не может заставить нас отказаться от принципа, что одина­ковые уравнения имеют одинаковые решения.

Теперь можно воспользоваться нашими предыдущими ре­зультатами о полях внутри полости различной формы в диэлект­риках, которые приведены на фиг. 36.1, для нахождения поля Н. Зная Н, можно определить и В. Например, поле Н внутри иглообразной полости, параллельной М (согласно результату, приведенному в § 1), будет тем же самым, что и поле Н внутри материала:

Но поскольку в нашей полости М равна нулю, то мы полу­чаем

С другой стороны, для дискообразной полости, перпендику­лярной М,

что в нашем случае превращается в

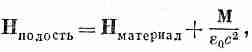
или в величинах В:

Наконец, для сферической полости аналогия с уравнением (36.3) дала бы

Результаты для магнитного поля, как видите, отличаются от тех, которые мы имели для электрического поля.

Конечно, их можно получить и более физически, непосред­ственно используя уравнения Максвелла. Например, уравне­ние (36.34) непосредственно следует из уравнения Ñ•B=0. (Возьмите гауссову поверхность, которая наполовину находит­ся в материале, а наполовину — вне его.) Подобным же обра­зом вы можете получить уравнение (36.33), воспользовавшись контурным интегралом по пути, который туда идет по полости, а назад возвращается через материал. Физически поле в полос­ти уменьшается благодаря поверхностным токам, определяемым как V X М. На вашу долю остается показать, что уравнение (36.35) можно получить, рассматривая эффекты поверхностных токов на границе сферической полости.

При нахождении равновесной намагниченности из уравне­ния (36.29) удобнее, оказывается, иметь дело с Н, поэтому мы пишем

В приближении сферической полости коэффициент Я следует взять равным ¹/₃, но, как вы увидите позже, нам придется пользоваться несколько другим его значением, а пока оставим его как подгоночный параметр. Кроме того, все поля мы возь­мем в одном и том же направлении, чтобы нам не нужно было заботиться о направлении векторов. Если бы теперь мы под­ставили уравнение (36.36) в (36.29), то получили бы уравнение, которое связывает намагниченность М с намагничивающим полем Н:

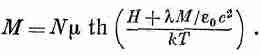
Однако это уравнение невозможно решить точно, так что мы будем делать это графически.

Сформулируем задачу в более общей форме, записывая уравнение (36.29) в виде

где М_нас — намагниченность насыщения, т. е. N_m, a x — вели­чина m B_a/kT. Зависимость М/М_нас от х показана на фиг. 36.13 (кривая а).

Фиг. 36.13. Графическое реше­ние уравнений (36.37) и (36.38),

Воспользовавшись еще уравнением (36.36) для В_а, можно записать х как функцию от М:

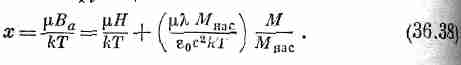
Эта формула определяет линейную зависимость между М/М_нас и х при любой величине Н. Прямая пересекается с осью х в точке x=mH/kT, и наклон ее равен e ₀с²kT/mlКМ_нас. Для любого частного зна­чения Н это будет пря­мая, подобная прямой b на фиг. 36.13. Пересечение кривых а и о дает нам решение для М/М_нас. Итак, задача решена.

Посмотрим теперь, годны ли эти решения при различных обстоятельствах. Начнем с H =0. Здесь представляются две возможности, показанные кривыми b₁ и b₂ на фиг. 36.14.

Фиг. 36.14. Определение намагниченности при Н=0.

Обра­тите внимание, что наклон прямой (36.38) пропорционален аб­солютной температуре Т. Таким образом, при высоких темпера­турах получится прямая, подобная b₁ Решением будет только М/М_нас=0. Иначе говоря, когда намагничивающее поле Я равно нулю, намагниченность тоже равна нулю. При низких температурах мы получили бы линию типа b₂ и стали возможны два решения для М/М_нас: одно М/М_нас=0, а другое М/М_нас порядка единицы. Оказывается, что только второе решение устойчиво, в чем можно убедиться, рассматривая малые вариа­ции в окрестности указанных решений.

В соответствии с этим при достаточно низких температурах магнитные материалы должны намагничиваться спонтанно. Короче говоря, когда тепловое движение достаточно мало, то взаимодействие между атомными магнитиками заставляет их выстраиваться параллельно друг другу, получается постоянно намагниченный материал, аналогичный пос­тоянно поляризованным сегнетоэлектрикам, о которых мы говорили в гл. 11 (вып. 5).

Если мы отправимся от высоких температур и начнем дви­гаться вниз, то при некой критической температуре, называемой температурой Кюри Т_c, неожиданно проявляется ферромагнит­ное поведение. Эта температура соответствует на фиг. 36.14 линии b₃, касательной к кривой а, наклон которой равен еди­нице. Так что температура Кюри определяется из равенства

При желании уравнение (36.38) можно записать в более прос­том виде через Т_c:

Что же получается для малых намагничивающих полей Н? Из фиг. 36.14 нетрудно понять, что получится, если нашу пря­мую линию сдвинуть немного направо. В случае низкой темпе­ратуры точка пересечения немного сдвинется направо по слабо наклоненной части кривой а и изменения М будут сравнительно невелики. Однако в случае высокой температуры точка пересе­чения побежит по крутой части кривой а и изменения М станут относительно быстрыми. Эту часть кривой мы фактически мо­жем приближенно заменить прямой линией а с единичным наклоном и написать

Теперь можно разрешить уравнение относительно М/М_нас:

Мы получаем закон, несколько напоминающий закон для па­рамагнетизма:

Отличие состоит, в частности, в том, что мы получили намагни­ченность как функцию Н, с учетом взаимодействия атомных магнитиков, однако главное то, что намагниченность обратно пропорциональна разности температур Т и Т_с, а не просто абсолютной температуре Т. Пренебрежение взаимодействием между соседними атомами соответствует l=0, что, согласно уравнению (36.39), означает Т_с= 0. Результат при этом полу­чится в точности таким же, как и в гл. 35.

Нашу теоретическую картину можно сверить с эксперимен­тальными данными для никеля. На опыте обнаружено, что ферромагнитные свойства никеля исчезают, когда температура поднимается выше 631° К. Это значение можно сравнить со значением Т_с, вычисленным из равенства (36.39). Вспоминая, что M_нас=m N, мы получаем

Из плотности и атомного веса никеля находим

N=9,1•10²⁸м^-3. А вычисление m, из уравнения (36.28) и подстановка l=¹/₃ дает

T_с=0,24°K.

Различие с экспериментом примерно в 2600 раз! Наша теория ферромагнетизма полностью провалилась!

Можно попытаться «подправить» нашу теорию, как это сде­лал Вейсс, предположив, что по каким-то неизвестным причи­нам К равно не ¹/₃, а (2600) •¹/₃, т. е. около 900. Оказывается, что подобная величина получается и для других ферромагнит­ных материалов типа железа. Вернемся к уравнению (36.36) и попробуем понять, что это может означать? Мы видим, что большая величина Я означает, что В_а (локальное поле, дейст­вующее на атом) должно быть больше, много больше, чем мы думали. Фактически, записывая Н = В-M/e₀c², мы получили

В соответствии с нашей первоначальной идеей, когда мы при­нимали l=¹/₃, локальная намагниченность М уменьшает эффективное поле В_а на величину — 2М/Зe₀. Даже если бы наша модель сферической полости была не очень хороша, мы все равно ожидали бы некоторого уменьшения. Вместо того чтобы объяснить явление ферромагнетизма, мы вынуждены считать, что намагниченность увеличивает локальное поле в огромное число раз: в тысячу и даже больше. По-видимому, не существует какого-то разумного способа для создания действующего на атом поля такой ужасной величины, ни даже поля нужного знака! Ясно, что наша «магнитная» теория ферромагнетизма потерпела досадный провал. Мы вынуждены заключить, что в ферромагнетизме мы имеем дело с какими-то не магнитными взаимодействиями между вращающимися электронами соседних атомов. Это взаимодействие должно порождать у соседних спинов сильную тенденцию к выстраиванию в одном направлении. Мы увидим позднее, что это взаимодействие связано с квантовой механикой и принципом запрета Паули. И, наконец, посмотрим, что происходит при низких темпе­ратурах, когда Т<T_с. Мы видели, что даже при Н=0 в этом случае должна существовать спонтанная намагниченность, определяемая пересечением кривых а и b₂ на фиг. 36.14. Если мы, изменяя наклон линии b₂, будем находить М для различ­ных температур, то получим теоретическую кривую, пока­занную на фиг. 36.15.

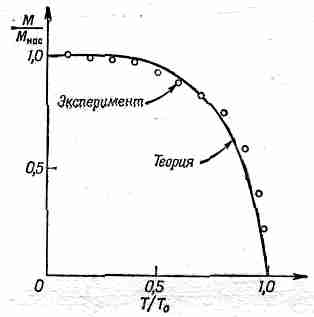
Фиг. 36.15. Зависимость спонтан­ной намагниченности никеля от тем­пературы.

Для всех ферромагнитных материалов, атомные моменты которых обусловлены одним электроном, эта кривая должна быть одной и той же. Для других материалов подобные кривые могут отличаться лишь немного.

В пределе, когда Т стремится к абсолютному нулю, М стре­мится к M_нac. При увеличении температуры намагниченность уменьшается, падая до нуля при температуре Кюри. Точками на фиг. 36.15 показаны экспериментальные данные для никеля. Они довольно хорошо ложатся на теоретическую кривую. Хотя мы и не понимаем лежащего в основе механизма, но общие свойства теории, по-видимому, все же правильны.

Но в нашей попытке понять ферромагнетизм есть еще одна неприятная несогласованность, которая должна нас заботить. Мы нашли, что выше некоторой температуры материал должен вести себя как парамагнитное вещество, намагниченность кото­рого пропорциональна Н (или В), а ниже этой температуры должна возникать спонтанная намагниченность. Но при пост­роении кривой намагничивания для железа мы этого как раз и не обнаружили. Железо становится постоянно намагниченным только после того, как мы его «намагнитим». А в соответствии с только что высказанными идеями оно должно намагничиваться само! Что же неверно? Оказывается, что если вы рассмотрите достаточно маленький кристалл железа или никеля, то увидите что он и впрямь полностью намагничен! А большой кусок железа состоит из массы таких маленьких областей, или «доменов», которые намагничены в различных направлениях, так что средняя намагниченность в большом масштабе оказывается равной нулю. Однако в каждом маленьком домене железо все же намагничивает само себя, причем М приблизительно равно M_нac. Как следствие этой доменной структуры свойства боль­шого куска материала должны быть совершенно отличны от микроскопических, как это и оказывается на самом деле.

* В системе, которой пользуется здесь автор, В=Н+1/e₀c² М, но

D=e₀E+P. В старой, доброй системе единиц писали В=m₀Н=(1/e₀c²)Н и

D=e₀Е или В=(Н+4pМ) и D=Е+4pР. Надо быть очень внима­тельным, когда формулы для магнетиков пишутся по аналогии с формулами для диэлектриков (ср. § 6).— Прим. ред.

Дата добавления: 2015-08-20